
| a2 |
| c |
| y2 |
| 4 |
| x2 |
| 3 |
| 5 |
| 2 |
| 3 |
| 2 |
| |PF1|2+|PF2|2-|F1F2|2 |
| 2×|PF2|×|PF1| |
| 3 |
| 5 |
| 4 |
| 5 |
| sin∠F1PF2 |
| cos∠F1PF2 |
| 4 |
| 3 |


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源:2007-2008学年广东省惠州一中高三(上)数学寒假作业5(理科)(解析版) 题型:选择题
 的左焦点为F,A(-a,0),B(0,b)为椭圆的两个顶点,若F到AB的距离等于
的左焦点为F,A(-a,0),B(0,b)为椭圆的两个顶点,若F到AB的距离等于 ,则椭圆的离心率为( )
,则椭圆的离心率为( )
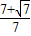


查看答案和解析>>
科目:高中数学 来源:2012-2013学年宁夏银川一中高三(下)第六次月考数学试卷(文科)(解析版) 题型:解答题
 的右焦点为F(2,0),M为椭圆的上顶点,O为坐标原点,且△MOF是等腰直角三角形.
的右焦点为F(2,0),M为椭圆的上顶点,O为坐标原点,且△MOF是等腰直角三角形. ).
).查看答案和解析>>
科目:高中数学 来源:2011-2012学年高二(上)周考数学试卷(10)(解析版) 题型:选择题
 的左焦点为F,A(-a,0),B(0,b)为椭圆的两个顶点,若F到AB的距离等于
的左焦点为F,A(-a,0),B(0,b)为椭圆的两个顶点,若F到AB的距离等于 ,则椭圆的离心率为( )
,则椭圆的离心率为( )



查看答案和解析>>
科目:高中数学 来源:2012年内蒙古包头市高考数学三模试卷(文科)(解析版) 题型:解答题
 的右焦点为F(2,0),M为椭圆的上顶点,O为坐标原点,且△MOF是等腰直角三角形.
的右焦点为F(2,0),M为椭圆的上顶点,O为坐标原点,且△MOF是等腰直角三角形. ).
).查看答案和解析>>
科目:高中数学 来源:高考数学一轮复习必备(第61课时):第八章 圆锥曲线方程-椭圆(解析版) 题型:选择题
 的左焦点为F,A(-a,0),B(0,b)为椭圆的两个顶点,若F到AB的距离等于
的左焦点为F,A(-a,0),B(0,b)为椭圆的两个顶点,若F到AB的距离等于 ,则椭圆的离心率为( )
,则椭圆的离心率为( )



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com