练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    某单位为了制定节能减排的目标，先调查了用电量y（度）与气温x (0C)之间的关系，随机统计了某4天的用电量与当天气温，并制作了对照表：
    气温(0C)
    		18
    		13
    		10
    		-1
    用电量（度）
    		24
    		34
    		38
    		64
     
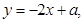    由表中数据，得线性回归方程则a=            ．
    60

    试题分析：先求得,再由线性回归方程必过点得到:.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

    某工厂为了对新研发的一种产品进行合理定价，将该产品按事先拟定的价格进行试销，得到如下数据:
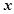    单价（元）
    		8
    		8.2
    		8.4
    		8.6
    		8.8
    		9
    销量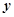（件）
    		90
    		84
    		83
    		80
    		75
    		68
     
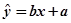    （1）根据上表可得回归直线方程中的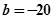，据此模型预报单价为10元时的销量为多少件?
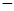    （2）预计在今后的销售中，销量与单价仍然服从（1）中的关系，且该产品的成本是4元/件，为使工厂获得最大利润，该产品的单价应定为多少元？（利润=销售收入成本）

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    一家面包房根据以往某种面包的销售记录，绘制了日销售量的频率分布直方图，如图所示：

    将日销售量落入各组的频率视为概率，并假设每天的销售量相互独立.
    （1）求在未来连续3天里，有连续2天的日销售量都不低于100个且另一天的日销售量低于50个的概率；
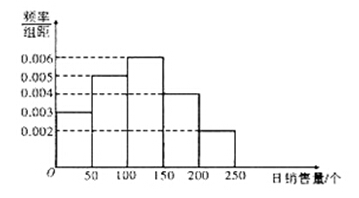
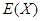    （2）用X表示在未来3天里日销售量不低于100个的天数，求随机变量X的分布列，期望及方差.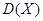

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    某企业为了监控产品质量，从产品流转均匀的生产线上每间隔10分钟抽取一个样本进行检测，这种抽样方法是（　　）
    A．抽签法B．随机数表法C．系统抽样法D．分层抽样法

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    某中学共有学生2000人，各年级男，女生人数如下表：
    一年级二年级三年级
    女生373xy
    男生377370z
    已知在全校学生中随机抽取1名，抽到高二年级女生的概率是0.19．
    （1）现用分层抽样的方法在全校抽取48名学生，问应在高三年级抽取多少名？
    （2）已知y≥245，z≥245，求高三年级中女生比男生多的概率．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    以下结论正确的是        
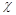    （1）根据2×2列联表中的数据计算得出2≥6.635, 而P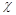（2≥6.635）≈0.01，则有99% 的把握认为两个分类变量有关系。
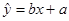    （2）在线性回归分析中，相关系数为r，|r|越接近于1，相关程度越大；|r|越小，相关程度越小。
    （3）在回归分析中，回归直线方程过点。 
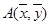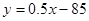    （4）在回归直线中，变量x=200时，变量y的值一定是15。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

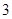    为了解某校今年准备报考飞行员学生的体重情况，将所得的数据整理后，画出了频率分布直方图(如图)，已知图中从左到右的前个小组的频率之比为，其中第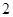小组的频数为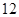，则报考飞行员的总人数是     ．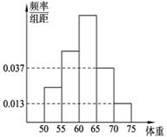

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    某商品销售量（件）与销售价格（元/件）负相关，则其回归方程可能是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    独立性检验中，假设H0：变量X与变量Y没有关系，则在H0成立的情况下，P(K2≥6.635)≈0.010表示的意义是（ ）
    A．在犯错误的概率不超过0.1%的前提下，认为“变量X与变量Y有关”
    B．在犯错误的概率不超过0.1%的前提下，认为“变量X与变量Y无关”
    C．有99%以上的把握认为“变量X与变量Y无关”
    D．有99%以上的把握认为“变量X与变量Y有关”

    查看答案和解析>>

    同步练习册答案