
例
(2005高考福建卷)已知函数![]() 的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为
的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为![]() . (Ⅰ)求函数
. (Ⅰ)求函数![]() 的解析式;
的解析式;
![]()
【思维分析】利用导数的几何意义解答。
解析:(Ⅰ)由![]() 的图象经过P(0,2),知d=2,所以
的图象经过P(0,2),知d=2,所以![]()
![]() 由在
由在![]() 处的切线方程是
处的切线方程是![]() ,知
,知
![]()
![]() 故所求的解析式是
故所求的解析式是![]()
【知识点归类点拔】导数的几何意义:函数y=f(x)在点![]() 处的导数,就是曲线y=(x)在点
处的导数,就是曲线y=(x)在点![]() 处的切线的斜率.由此,可以利用导数求曲线的切线方程.具体求法分两步: (1)求出函数y=f(x)在点
处的切线的斜率.由此,可以利用导数求曲线的切线方程.具体求法分两步: (1)求出函数y=f(x)在点![]() 处的导数,即曲线y=f(x)在点
处的导数,即曲线y=f(x)在点![]() 处的切线的斜率;(2)在已知切点坐标和切线斜率的条件下,求得切线方程为
处的切线的斜率;(2)在已知切点坐标和切线斜率的条件下,求得切线方程为 ![]() 特别地,如果曲线y=f(x)在点
特别地,如果曲线y=f(x)在点![]() 处的切线平行于y轴,这时导数不存,根据切线定义,可得切线方程为
处的切线平行于y轴,这时导数不存,根据切线定义,可得切线方程为![]() 。利用导数的几何意义作为解题工具,有可能出现在解析几何综合试题中,复习时要注意到这一点.
。利用导数的几何意义作为解题工具,有可能出现在解析几何综合试题中,复习时要注意到这一点.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:高中数学 来源: 题型:
【练】
(1)(2005高考北京卷)已知函数f(x)=-x3+3x2+9x+a, (I)求f(x)的单调递减区间;(II)若f(x)在区间[-2,2]上的最大值为20,求它在该区间上的最小值.答案:(1)(-∞,-1),(3,+∞)(2)-7
查看答案和解析>>
科目:高中数学 来源:2012年人教A版高中数学必修三2.2用样本估计总体练习卷(一)(解析版) 题型:选择题
(2009年高考福建卷)一个容量为100的样本,其数据的分组与各组的频数如下:
|
组别 |
(0,10] |
(10,20] |
(20,30] |
(30,40] |
(40,50] |
(50,60] |
(60,70] |
|
频数 |
12 |
13 |
24 |
15 |
16 |
13 |
7 |
则样本数据落在(10,40]上的频率为( )
A.0.13 B.0.39
C.0.52 D.0.64
查看答案和解析>>
科目:高中数学 来源:2012年人教A版高中数学必修一3.1函数与方程练习卷(一)(解析版) 题型:选择题
(2010年高考福建卷)函数f(x)=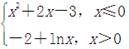 的零点个数为( )
的零点个数为( )
A.0 B.1
C.2 D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com