
【题目】已知函数f(x)=ex-a+lnx。
(1)若a=1,求证:当x>1时,f(x)>2x-1
(2)若存在x0≥e,使f(x)<2lnx0,求实数a的取值范围.
【答案】(1)见解析(2)见解析
【解析】试题分析:
(1)由题意对函数求导,然后构造函数![]() ,结合函数的性质即可证得题中的结论;
,结合函数的性质即可证得题中的结论;
(2)结合题意构造函数![]() ,结合其导函数的性质可得实数a的取值范围是
,结合其导函数的性质可得实数a的取值范围是![]() .
.
试题解析:
(1)a=1时,f(x)=ex-1+lnx, ![]() =ex-1+
=ex-1+![]()
设g(x)=ex-1+lnx-2x+1, ![]() =ex-1+
=ex-1+![]() -2
-2
![]() =ex-1-
=ex-1-![]() ,x>1,ex-1>1,0>
,x>1,ex-1>1,0>![]() <1.
<1. ![]() =ex-1-
=ex-1-![]() >0
>0
![]() 在(1,+∞)递增,又g’(1)=0,∴x>1时,
在(1,+∞)递增,又g’(1)=0,∴x>1时, ![]()
g(x)在(1,+∞)递增,x>1时,g(x)>g(1)=0,即ex+lnx-2x+1>0
x>1时,ex+lnx>2x-1,即f(x)>2x-1
(2)若存在x0≥e,使f(x0)<2lnx0,即ex0-a<lnx0
即存在x0>e,使ea>![]()
设h(x)=![]() (x≥e),则h’(x)=
(x≥e),则h’(x)=![]()
u=lnx-![]() ,u’=
,u’=![]() 在[e,+∞)递增。
在[e,+∞)递增。
x=e时,u=1-![]() >0,所以u>0在[e,+00)恒成立,
>0,所以u>0在[e,+00)恒成立,
h’(x)>0,在[e,+00)恒成立,所以h(x)[e,+∞)递增
x≥e,时h(x)min=h(e)=ee
需ea>ee![]() a>e
a>e


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】假设乒乓球团体比赛的规则如下:进行5场比赛,除第3场为双打外,其余各场为单打,参赛的每个队选出3名运动员参加比赛,每个队员打两场,且第1,2场与第4,5场不能是某个运动员连续比赛.某队有4名乒乓球运动员,其中 ![]() 不适合双打,则该队教练安排运动员参加比赛的方法共有种
不适合双打,则该队教练安排运动员参加比赛的方法共有种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的方程为
的方程为![]() ,点
,点![]() 是抛物线
是抛物线![]() 上到直线
上到直线![]() 距离最小的点,点
距离最小的点,点![]() 是抛物线上异于点
是抛物线上异于点![]() 的点,直线
的点,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,过点
,过点![]() 与
与![]() 轴平行的直线与抛物线
轴平行的直线与抛物线![]() 交于点
交于点![]() .
.
(Ⅰ)求点![]() 的坐标;
的坐标;
(Ⅱ)证明直线![]() 恒过定点,并求这个定点的坐标.
恒过定点,并求这个定点的坐标.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知指数函数y=g(x)满足:g(3)=27,定义域为R的函数f(x)= ![]() 是奇函数.
是奇函数.
(1)确定y=g(x),y=f(x)的解析式;
(2)若h(x)=kx﹣g(x)在(0,1)上有零点,求k的取值范围;
(3)若对任意的t∈(1,4),不等式f(2t﹣3)+f(t﹣k)>0恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的首项a1=3,且公差d≠0,其前n项和为Sn , 且a1 , a4 , a13分别是等比数列{bn}的b2 , b3 , b4 . (Ⅰ)求数列{an}与{bn}的通项公式;
(Ⅱ)证明 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场欲经销某种商品,考虑到不同顾客的喜好,决定同时销售A、B两个品牌,根据生产厂家营销策略,结合本地区以往经销该商品的大数据统计分析,A品牌的销售利润y1与投入资金x成正比,其关系如图1所示,B品牌的销售利润y2与投入资金x的算术平方根成正比,其关系如图2所示(利润与资金的单位:万元). 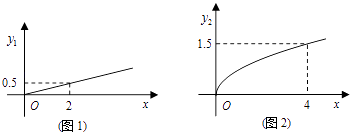
(1)分别将A、B两个品牌的销售利润y1、y2表示为投入资金x的函数关系式;
(2)该商场计划投入5万元经销该种商品,并全部投入A、B两个品牌,问:怎样分配这5万元资金,才能使经销该种商品获得最大利润,其最大利润为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的可导函数f(x)的导函数为f′(x),满足f′(x)>f(x),且f(x+2)为奇函数,f(4)=﹣1,则不等式f(x)<ex的解集为( )
A.(﹣2,+∞)
B.(0,+∞)
C.(1,+∞)
D.(﹣∞,0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com