
【题目】如图,已知⊙O中,直径AB垂直于弦CD,垂足为M,P是CD延长线上一点,PE切⊙O于点E,连接BE交CD于点F,证明:
(1)∠BFM=∠PEF;
(2)PF2=PD·PC.
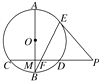
【答案】(1)见解析(2)见解析
【解析】试题分析:(1)如图所示,连接OE.利用切线的性质可得:OE⊥PE,于是∠PEF+∠OEF=90°.由已知AB⊥CD,可得∠OBF+∠BFM=90°.由同圆的半径相等可得∠OBF=∠OEB.即可得出结论.
(2)利用(1)可得∠PEF=∠PFE.于是PE=PF.利用“切割线定理”可得PE2=PDPC.即可.
试题解析:
证明:(1)连接OE.
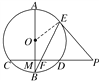
∵PE切⊙O于点E,
∴OE⊥PE.
∴∠PEF+∠FEO=90°.
又∵AB⊥CD,
∴∠B+∠BFM=90°.
又∵∠B=∠FEO,
∴∠BFM=∠PEF.
(2)∵∠EFP=∠BFM,
∴∠EFP=∠PEF.
∴PE=PF.
又∵PE2=PD·PC,
∴PF2=PD·PC.


 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:高中数学 来源: 题型:
【题目】已知等差数列{![]() }的前n项和为Sn,公差d>0,且
}的前n项和为Sn,公差d>0,且![]() ,
, ![]() ,公比为q(0<q<1)的等比数列{
,公比为q(0<q<1)的等比数列{![]() }中,
}中, ![]()
(1)求数列{![]() },{
},{![]() }的通项公式
}的通项公式![]() ,
, ![]() ;
;
(2)若数列{![]() }满足
}满足![]() ,求数列{
,求数列{![]() }的前n项和Tn。
}的前n项和Tn。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由小到大排列的一组数据x1 , x2 , x3 , x4 , x5 , 其中每个数据都小于﹣1,则样本1,x1 , ﹣x2 , x3 , ﹣x4 , x5的中位数为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,侧棱AA1⊥底面ABC,AB=AC,D,D1分别是线段BC,B1C1的中点,P是线段AD上异于端点的点. 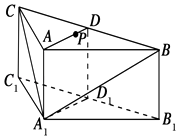
(1)在平面ABC内,试作出过点P与平面A1BC平行的直线l,并说明理由;
(2)证明:直线l⊥平面ADD1A1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着资本市场的强势进入,互联网共享单车“忽如一夜春风来”,遍布了一二线城市的大街小巷.为了解共享单车在![]() 市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中抽取了200人进行抽样分析,得到表格:(单位:人)
市的使用情况,某调查机构借助网络进行了问卷调查,并从参与调查的网友中抽取了200人进行抽样分析,得到表格:(单位:人)
经常使用 | 偶尔或不用 | 合计 | |
30岁及以下 | 70 | 30 | 100 |
30岁以上 | 60 | 40 | 100 |
合计 | 130 | 70 | 200 |
(1)根据以上数据,能否在犯错误的概率不超过0.15的前提下认为![]() 市使用共享单车情况与年龄有关?
市使用共享单车情况与年龄有关?
(2)现从所抽取的30岁以上的网友中利用分层抽样的方法再抽取5人.
(i)分别求这5人中经常使用、偶尔或不用共享单车的人数;
(ii)从这5人中,再随机选出2人赠送一件礼品,求选出的2人中至少有1人经常使用共享单车的概率.
参考公式:  ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() .
.
(1)当 ![]() 时,求函数f(x)的取值范围;
时,求函数f(x)的取值范围;
(2)将f(x)的图象向左平移 ![]() 个单位得到函数g(x)的图象,求g(x)的单调递增区间.
个单位得到函数g(x)的图象,求g(x)的单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个口袋内有4个不同的红球,6个不同的白球,
(1)从中任取4个球,红球的个数不比白球少的取法有多少种?
(2)若取一个红球记2分,取一个白球记1分,从中任取5个球,使总分不少于7分的取法有多少种?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂甲、乙两个车间包装同一种产品,在自动包装传送带上每隔1小时抽一包产品,称其重量(单位:克)是否合格,分别记录抽查数据,获得重量数据的茎叶图如图.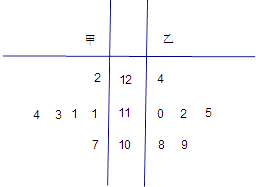
(1)根据样品数据,计算甲、乙两个车间产品重量的均值与方差,并说明哪个车间的产品的重量相对较稳定;
(2)若从乙车间6件样品中随机抽取两件,求所抽取的两件样品的重量之差不超过2克的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com