
【题目】已知实数![]() ,
,![]() 满足
满足![]() ,实数
,实数![]() ,
,![]() 满足
满足![]() ,则
,则![]() 的最小值为__________.
的最小值为__________.
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:
【题目】如图,已知圆心坐标为( ![]() ,1)的圆M与x轴及直线y=
,1)的圆M与x轴及直线y= ![]() x分别相切于A,B两点,另一圆N与圆M外切、且与x轴及直线y=
x分别相切于A,B两点,另一圆N与圆M外切、且与x轴及直线y= ![]() x分别相切于C、D两点.
x分别相切于C、D两点. 
(1)求圆M和圆N的方程;
(2)过点B作直线MN的平行线l,求直线l被圆N截得的弦的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l过点M(1,2),且直线l与x轴正半轴和y轴的正半轴交点分别是A、B,(如图,注意直线l与坐标轴的交点都在正半轴上) 
(1)若三角形AOB的面积是4,求直线l的方程.
(2)求过点N(0,1)且与直线l垂直的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD﹣A1B1C1D1中,E、F、G分别是棱A1B1、BB1、B1C1的中点,则下列结论中:
①FG⊥BD
②B1D⊥面EFG
③面EFG∥面ACC1A1
④EF∥面CDD1C1
正确结论的序号是( )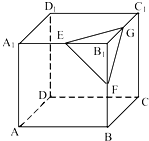
A.①和②
B.②和④
C.①和③
D.③和④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若ABC的三个顶点的坐标分别为A(4,0),B(6,7),C(0,3).
①求BC边上的高所在直线的方程;
②求BC边上的中线所在的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市对创“市级优质学校”的甲、乙两所学校复查验收,对办学的社会满意度一项评价随机访问了![]() 位市民,根据这
位市民,根据这![]() 位市民对这两所学校的评分(评分越高表明市民的评价越好),绘制茎叶图如下:
位市民对这两所学校的评分(评分越高表明市民的评价越好),绘制茎叶图如下:
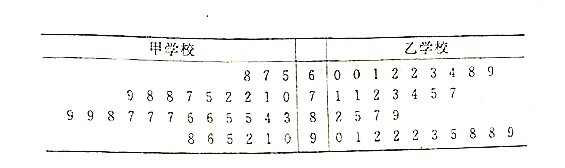
(1)分别估计该市的市民对甲、乙两所学校评分的中位数;
(2)分别估计该市的市民对甲、乙两所学校的评分不低于![]() 分的概率;
分的概率;
(3)根据茎叶图分析该市的市民对甲、乙两所学校的评价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥的侧棱PD⊥底面ABCD,且底面ABCD是直角梯形,AD⊥CD,AB∥CD,AB=AD= ![]() CD=2,点M在侧棱上.
CD=2,点M在侧棱上.
(1)求证:BC⊥平面BDP;
(2)若侧棱PC与底面ABCD所成角的正切值为 ![]() ,点M为侧棱PC的中点,求异面直线BM与PA所成角的余弦值.
,点M为侧棱PC的中点,求异面直线BM与PA所成角的余弦值. 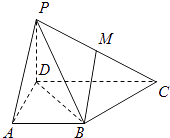
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com