
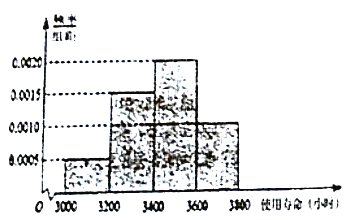
【题目】某公司租用一个门店作展馆,准备对其公司生产的某型产品进行为期一年的展出。为此,需对门店进行装修,展出结束,门店不再使用,现市面上有某品牌的![]() 型和
型和![]() 型两种节能灯,假定
型两种节能灯,假定![]() 型节能灯使用寿命都超过
型节能灯使用寿命都超过![]() 小时,经销商对
小时,经销商对![]() 型节能灯使用寿命进行了调查统计,得到如下频率分布直方图:
型节能灯使用寿命进行了调查统计,得到如下频率分布直方图:
门店装修时,需安装该品牌节能灯![]() 支(同种型号).经了解,
支(同种型号).经了解,![]() 型
型![]() 瓦和B型
瓦和B型![]() 瓦的两种节能灯照明效果相当,都适合安装。已知
瓦的两种节能灯照明效果相当,都适合安装。已知![]() 型和
型和![]() 型节能灯每支的价格分别为
型节能灯每支的价格分别为![]() 元、
元、![]() 元,当地商业电价为
元,当地商业电价为![]() 元/千瓦时。假定该店面一年周转期的照明时间为
元/千瓦时。假定该店面一年周转期的照明时间为![]() 小时,若正常营业期间灯坏了立即购买同型灯管更换。(用频率估计概率)
小时,若正常营业期间灯坏了立即购买同型灯管更换。(用频率估计概率)
(1)根据频率直方图估算B型节能灯的平均使用寿命;
(2)根据统计知识,若一支灯管一年内需要更换的概率为![]() ,那么支灯管一年内估计需要更换
,那么支灯管一年内估计需要更换![]() 支.若该商家新店面全部安装
支.若该商家新店面全部安装![]() 型节能灯,试估计一年内需更换的支数;
型节能灯,试估计一年内需更换的支数;
(3)若只考虑灯的成本和消耗电费,你认为该商家应选择哪种型号的节能灯,请说明理由.
【答案】(1)![]() 小时;(2)
小时;(2)![]() ;(3)应选择
;(3)应选择![]() 型节能灯.
型节能灯.
【解析】
(1)利用频率分布图的平均数的公式估算B型节能灯的平均使用寿命;(2) 使用寿命不超过![]() 小时的频率为
小时的频率为![]() ,将频率视为概率,每支灯管需要更换的概率为
,将频率视为概率,每支灯管需要更换的概率为![]() ,故估计一年内
,故估计一年内![]() 支
支![]() 型节能灯需更换的支数为
型节能灯需更换的支数为![]() ;(3)分别计算A型B型灯的花费,再确定选择哪种型号的节能灯.
;(3)分别计算A型B型灯的花费,再确定选择哪种型号的节能灯.
(1)由图可知,各组中值依次为![]() ,
,![]() ,
,![]() ,
,![]() ,对应的频率依次为
,对应的频率依次为![]() ,
,![]() ,
,![]() ,
,![]() ,故
,故![]() 型节能灯的平均使用寿命为:
型节能灯的平均使用寿命为:
![]() .(小时)
.(小时)
(2)由图可知,使用寿命不超过![]() 小时的频率为
小时的频率为![]() ,将频率视为概率,每支灯管需要更换的概率为
,将频率视为概率,每支灯管需要更换的概率为![]() ,故估计一年内
,故估计一年内![]() 支
支![]() 型节能灯需更换的支数为
型节能灯需更换的支数为![]() ,
,
(3)若选择![]() 型节能灯,一年共需花费
型节能灯,一年共需花费![]() 元;
元;
若选择![]() 型节能灯,一年共需花费
型节能灯,一年共需花费![]() 元,
元,
因为![]() ,所以该商家应选择
,所以该商家应选择![]() 型节能灯.
型节能灯.


科目:高中数学 来源: 题型:
【题目】某部门在同一上班高峰时段对甲、乙两地铁站各随机抽取了50名乘客,统计其乘车等待时间(指乘客从进站口到乘上车的时间,乘车等待时间不超过40分钟).将统计数据按![]() 分组,制成频率分布直方图:
分组,制成频率分布直方图:
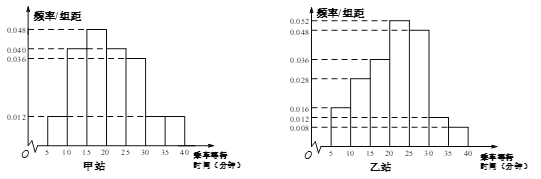
假设乘客乘车等待时间相互独立.
(1)在上班高峰时段,从甲站的乘客中随机抽取1人,记为![]() ;从乙站的乘客中随机抽取1人,记为
;从乙站的乘客中随机抽取1人,记为![]() .用频率估计概率,求“乘客
.用频率估计概率,求“乘客![]() ,
,![]() 乘车等待时间都小于20分钟”的概率;
乘车等待时间都小于20分钟”的概率;
(2)从上班高峰时段,从乙站乘车的乘客中随机抽取3人,![]() 表示乘车等待时间小于20分钟的人数,用频率估计概率,求随机变量
表示乘车等待时间小于20分钟的人数,用频率估计概率,求随机变量![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知变量![]() 、
、![]() 之间的线性回归方程为
之间的线性回归方程为![]() ,且变量
,且变量![]() 、
、![]() 之间的一-组相关数据如下表所示,则下列说法错误的是( )
之间的一-组相关数据如下表所示,则下列说法错误的是( )
|
|
|
|
|
|
|
|
|
|
A.可以预测,当![]() 时,
时,![]() B.
B.![]()
C.变量![]() 、
、![]() 之间呈负相关关系D.该回归直线必过点
之间呈负相关关系D.该回归直线必过点![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆锥![]() 如图①所示,图②是它的正(主)视图.已知圆
如图①所示,图②是它的正(主)视图.已知圆![]() 的直径为
的直径为![]() ,
, ![]() 是圆周上异于
是圆周上异于![]() 的一点,
的一点, ![]() 为
为![]() 的中点.
的中点.
(I)求该圆锥的侧面积S;
(II)求证:平面![]() ⊥平面
⊥平面![]() ;
;
(III)若∠CAB=60°,在三棱锥![]() 中,求点
中,求点![]() 到平面
到平面![]() 的距离.
的距离.
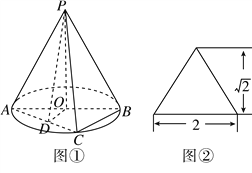
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】艾滋病是一种危害性极大的传染病,由感染艾滋病病毒![]() 病毒
病毒![]() 引起,它把人体免疫系统中最重要的CD4T淋巴细胞作为主要攻击目标,使人体丧失免疫功能
引起,它把人体免疫系统中最重要的CD4T淋巴细胞作为主要攻击目标,使人体丧失免疫功能![]() 下表是近八年来我国艾滋病病毒感染人数统计表:
下表是近八年来我国艾滋病病毒感染人数统计表:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代码x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
感染者人数 |
|
|
|
|
|
|
| 85 |
![]() 请根据该统计表,画出这八年我国艾滋病病毒感染人数的折线图;
请根据该统计表,画出这八年我国艾滋病病毒感染人数的折线图;
![]() 请用相关系数说明:能用线性回归模型拟合y与x的关系;
请用相关系数说明:能用线性回归模型拟合y与x的关系;
![]() 建立y关于x的回归方程
建立y关于x的回归方程![]() 系数精确到
系数精确到![]() ,预测2019年我国艾滋病病毒感染人数.
,预测2019年我国艾滋病病毒感染人数.
参考数据:![]() ;
;![]() ,
,![]() ,
,![]() ,
,
参考公式:相关系数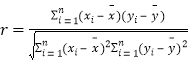 ,
,
回归方程![]() 中,
中,![]()
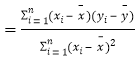 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在坐标原点,焦点在x轴上,左顶点为A,左焦点为![]() ,点
,点![]() 在椭圆C上,直线
在椭圆C上,直线![]() 与椭圆C交于E,F两点,直线AE,AF分别与y轴交于点M,N
与椭圆C交于E,F两点,直线AE,AF分别与y轴交于点M,N
![]() Ⅰ
Ⅰ![]() 求椭圆C的方程;
求椭圆C的方程;
![]() Ⅱ
Ⅱ![]() 在x轴上是否存在点P,使得无论非零实数k怎样变化,总有
在x轴上是否存在点P,使得无论非零实数k怎样变化,总有![]() 为直角?若存在,求出点P的坐标,若不存在,请说明理由.
为直角?若存在,求出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】太极图被称为“中华第一图”.广为人知的太极图,其形状如阴阳两鱼互抱在一起,因而被称为“阴阳鱼太极鱼”.已知![]() 或
或 ,下列命题中:①
,下列命题中:①![]() 在平面直角坐标系中表示的区域的面积为
在平面直角坐标系中表示的区域的面积为![]() ;②
;②![]() ,使得
,使得![]() ;③
;③![]() ,都有
,都有![]() 成立;④设点
成立;④设点![]() ,则
,则![]() 的取值范围是
的取值范围是![]() .其中真命题的个数为( )
.其中真命题的个数为( )

A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系.已知曲线C的极坐标方程为ρ(1-cos2θ)=8cosθ,直线ρcosθ=1与曲线C相交于M,N两点,直线l过定点P(2,0)且倾斜角为α,l交曲线C于A,B两点.
(1)把曲线C化成直角坐标方程,并求|MN|的值;
(2)若|PA|,|MN|,|PB|成等比数列,求直线l的倾斜角α.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平面![]() 平面
平面![]() ,
,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,四边形
,四边形![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
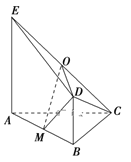
(1求异面直角![]() 与
与![]() 所成角的大小;
所成角的大小;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com