
【题目】已知幂函数y=f(x)的图象过点(8,m)和(9,3).
(Ⅰ)求m的值;
(Ⅱ)若函数g(x)=logaf(x)(a>0,a≠1)在区间[16,36]上的最大值比最小值大1,求实数a的值.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ) ![]()
【解析】试题分析:(Ⅰ)由题意y=f(x)是幂函数,设设f(x)=xα,图象过点(8,m)和(9,3)即可求解m的值.
(Ⅱ)函数g(x)=logaf(x)在区间[16,36]上的最大值比最小值大1,对底数进行讨论,利用单调性求最值,可得实数a的值.
试题解析: 解:(Ⅰ)由题意,y=f(x)是幂函数,设f(x)=xα,图象过点(8,m)和(9,3)
可得9α=3,所以α=![]() ,
,
故f(x)=![]() .
.
∴m=f(8)=2![]() .
.
故得m的值为2![]() .
.
(Ⅱ)函数g(x)=logaf(x)即为g(x)=![]() ,
,
∵x在区间[16,36]上,
∴![]() ∈[4,6],
∈[4,6],
①当0<a<1时,g(x)min=loga6,g(x)max=loga4,
由loga4﹣loga6=loga![]() =1,
=1,
解得a=![]() ;
;
②当a>1时,g(x)min=loga4,g(x)max=loga6,
由loga6﹣loga4=loga![]() =1,
=1,
解得a=![]() .
.
综上可得,实数a的值为![]() 或
或![]() .
.


 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:
【题目】在边长为60cm的正方形铁片的四角切去相等的正方形,再把它的边沿虚线折起(如图),做成一个无盖的方底箱子,箱底的边长是多少时,箱子的容积最大?最大容积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
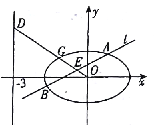
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() ,如图所示,斜率为
,如图所示,斜率为![]() 且不过原点的直线
且不过原点的直线![]() 交椭圆
交椭圆![]() 于两点
于两点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,射线
,射线![]() 交椭圆
交椭圆![]() 于点
于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
(1)求![]() 的最小值;
的最小值;
(2)若![]() ,求证:直线
,求证:直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了解广告投入对销售收益的影响,在若干地区各投入4万元广告费,并将各地的销售收益绘制成频率分布直方图(如图所示),由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的. 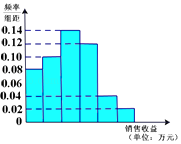
(1)根据频率分布直方图计算各小长方形的宽度;
(2)估计该公司投入4万元广告费之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值)
(3)该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:
广告投入x(单位:万元) | 1 | 2 | 3 | 4 | 5 |
销售收益y(单位:万元) | 2 | 3 | 2 | 7 |
表格中的数据显示,x与y之间存在线性相关关系,请将(2)的结果填入空白栏,并计算y关于x的回归方程.
回归直线的斜率和截距的最小二乘法估计公式分别为  ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】排列组合
(1)7位同学站成一排,甲、乙两同学必须相邻的排法共有多少种?
(2)7位同学站成一排,甲、乙和丙三个同学都不能相邻的排法共有多少种?
(3)7位同学站成一排,甲不站排头,乙不站排尾,不同站法种数有多少种?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了得到函数 ![]() 的图象,只要将函数y=sin2x的图象( )
的图象,只要将函数y=sin2x的图象( )
A.向右平移 ![]() 个单位长度
个单位长度
B.向左平移 ![]() 个单位长度
个单位长度
C.向右平移 ![]() 个单位长度
个单位长度
D.向左平移 ![]() 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为
的定义域为![]() ,其中
,其中![]() 为常数;
为常数;
(1)若![]() ,且
,且![]() 是奇函数,求
是奇函数,求![]() 的值;
的值;
(2)若![]() ,
, ![]() ,函数
,函数![]() 的最小值是
的最小值是![]() ,求
,求![]() 的最大值;
的最大值;
(3)若![]() ,在
,在![]() 上存在
上存在![]() 个点
个点![]()
![]() ,满足
,满足![]() ,
, ![]() ,
,
![]() ,使得
,使得![]() ,
,
求实数![]() 的取值范围;
的取值范围;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com