
【题目】已知等差数列{an}的各项均为正数,Sn为等差数列{an}的前n项和,![]() .
.
(1)求数列{an}的通项an;
(2)设bn=an3n,求数列{bn}的前n项和Tn.
【答案】(1)![]() .(2)
.(2)![]()
【解析】
(1)先设等差数列{an}的公差为d(d>0),然后根据等差数列的通项公式及已知条件可列出关于d的方程,解出d的值,即可得到数列{an}的通项an;
(2)先根据第(1)题的结果计算出数列{bn}的通项公式,然后运用错位相减法计算前n项和Tn.
(1)由题意,设等差数列{an}的公差为d(d>0),则
a4a5=(1+3d)(1+4d)=11,
整理,得12d2+7d﹣10=0,
解得d![]() (舍去),或d
(舍去),或d![]() ,
,
∴an=1![]() (n﹣1)
(n﹣1)![]() ,n∈N*.
,n∈N*.
(2)由(1)知,bn=an3n![]() 3n=(2n+1)3n﹣1,
3n=(2n+1)3n﹣1,
∴Tn=b1+b2+b3+…+bn=3×1+5×31+7×32+…+(2n+1)3n﹣1,
∴3Tn=3×31+5×32+…+(2n﹣1)3n﹣1+(2n+1)3n,
两式相减,可得:
﹣2Tn=3×1+2×31+2×32+…+23n﹣1﹣(2n+1)3n
=3+2×(31+32+…+3n﹣1)﹣(2n+1)3n
=3+2![]() (2n+1)3n
(2n+1)3n
=﹣2n3n,
∴Tn=n3n.


 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:
【题目】如图是一幅招贴画的示意图,其中ABCD是边长为![]() 的正方形,周围是四个全等的弓形.已知O为正方形的中心,G为AD的中点,点P在直线OG上,弧AD是以P为圆心、PA为半径的圆的一部分,OG的延长线交弧AD于点H.设弧AD的长为
的正方形,周围是四个全等的弓形.已知O为正方形的中心,G为AD的中点,点P在直线OG上,弧AD是以P为圆心、PA为半径的圆的一部分,OG的延长线交弧AD于点H.设弧AD的长为![]() ,
,![]() .
.
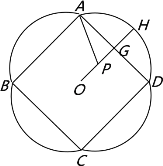
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)定义比值![]() 为招贴画的优美系数,当优美系数最大时,招贴画最优美.证明:当角
为招贴画的优美系数,当优美系数最大时,招贴画最优美.证明:当角![]() 满足:
满足:![]() 时,招贴画最优美.
时,招贴画最优美.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点坐标为
的焦点坐标为![]()
(1)求抛物线方程;
(2)过直线![]() 上一点
上一点![]() 作抛物线的切线切点为A,B
作抛物线的切线切点为A,B
①设直线PA、AB、PB的斜率分别为![]() ,求证:
,求证:![]() 成等差数列;
成等差数列;
②若以切点B为圆心r为半径的圆与抛物线C交于D,E两点且D,E关于直线AB对称,求点P横坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. “f(0)![]() ”是“函数f(x)是奇函数”的充要条件
”是“函数f(x)是奇函数”的充要条件
B. 若p:![]() ,
,![]() ,则
,则![]() :
:![]() ,
,![]()
C. “若![]() ,则
,则![]() ”的否命题是“若
”的否命题是“若![]() ,则
,则![]() ”
”
D. 若![]() 为假命题,则p,q均为假命题
为假命题,则p,q均为假命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A是抛物线E:y2=2px(p>0)上的一点,以点A和点B(2,0)为直径两端点的圆C交直线x=1于M,N两点.
(1)若|MN|=2,求抛物线E的方程;
(2)若0<p<1,抛物线E与圆(x﹣5)2+y2=9在x轴上方的交点为P,Q,点G为PQ的中点,O为坐标原点,求直线OG斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从甲地到乙地要经过3个十字路口,设各路口信号灯工作相互独立,且在各路口遇到红灯的概率分别为![]() .
.
(Ⅰ)设![]() 表示一辆车从甲地到乙地遇到红灯的个数,求随机变量
表示一辆车从甲地到乙地遇到红灯的个数,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)若有2辆车独立地从甲地到乙地,求这2辆车共遇到1个红灯的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·全国卷Ⅲ文,18)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
最高气温 | [10,15) | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) |
天数 | 2 | 16 | 36 | 25 | 7 | 4 |
以最高气温位于各区间的频率估计最高气温位于该区间的概率.
(1)估计六月份这种酸奶一天的需求量不超过300瓶的概率;
(2)设六月份一天销售这种酸奶的利润为Y(单位:元).当六月份这种酸奶一天的进货量为450瓶时,写出Y的所有可能值,并估计Y大于零的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是正方形,侧面
是正方形,侧面![]() 底面
底面![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 中点,
中点,![]() .
.

(Ⅰ)求证:![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)在棱![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 平面
平面![]() ?若存在,指出点
?若存在,指出点![]() 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com