解:361°是第一象限角,但不是锐角,故(1)第一象限角是锐角错误;
∵角a终边经过点(a,a)时,当a=-1时,sina+cosa=-

,故(2)角a终边经过点(a,a)时,sina+cosa=

错误;
若y=

sin(ωx)的最小正周期为4π,则ω=±

,故(3)若y=

sin(ωx)的最小正周期为4π,则ω=

错误;
若cos(α+β)=-1,则sin(α+β)=0,则sin(2α+β)+sinβ=sin[(α+β)+α]+sin[(α+β)-α]=2sin(α+β)cos(α+β)=0,故(4)正确;
若

∥

,则有且只有一个实数λ,使

=λ

.当

=

时不成立,故(5)错误;
若定义在R上函数f(x)满足f(x+1)=-f(x),则y=f(x)是周期为2的周期函数,故(6)正确;
故答案为:(4)、(6)
分析:根据象限角的定义、三角函数的定义、函数周期的确定、两角和与差的正弦公式、向量平行(共线)的充要条件、函数的周期的确定方法,我们逐一对已知中的四个结论进行判断,即可得到答案.
点评:本题考查的知识点是命题的真假判断与应用,函数的周期性,平行向量与共线向量,终边相同的角,象限角、轴线角,三角函数的周期性及其求法,属于基础题型,真正理解和掌握相关的定义是解答本题的关键.


 sin(ωx)的最小正周期为4π,则ω=
sin(ωx)的最小正周期为4π,则ω=
 ∥
∥ ,则有且只有一个实数λ,使
,则有且只有一个实数λ,使 =λ
=λ .
. ,故(2)角a终边经过点(a,a)时,sina+cosa=
,故(2)角a终边经过点(a,a)时,sina+cosa= 错误;
错误; sin(ωx)的最小正周期为4π,则ω=±
sin(ωx)的最小正周期为4π,则ω=± ,故(3)若y=
,故(3)若y= sin(ωx)的最小正周期为4π,则ω=
sin(ωx)的最小正周期为4π,则ω= 错误;
错误; ∥
∥ ,则有且只有一个实数λ,使
,则有且只有一个实数λ,使 =λ
=λ .当
.当 =
= 时不成立,故(5)错误;
时不成立,故(5)错误;

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案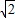
 sin(ωx)的最小正周期为4π,则ω=
sin(ωx)的最小正周期为4π,则ω=
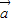 ∥
∥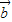 ,则有且只有一个实数λ,使
,则有且只有一个实数λ,使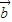 =λ
=λ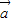 .
.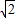
 sin(ωx)的最小正周期为4π,则ω=
sin(ωx)的最小正周期为4π,则ω=
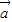 ∥
∥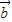 ,则有且只有一个实数λ,使
,则有且只有一个实数λ,使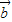 =λ
=λ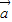 .
.