
【题目】在亚丁湾海域执行护航任务的中国海军“徐州”舰,在A处收到某商船在航行中发出求救信号后,立即测出该商船在方位角方位角(是从某点的指北方向线起,依顺时针方向到目标方向线之间的水平夹角)为45°、距离A处为10 n mile的C处,并测得该船正沿方位角为105°的方向,以9 n mile/h的速度航行,“徐州”舰立即以21 n mile/h的速度航行前去营救.
(1)“徐州”舰最少需要多少时间才能靠近商船?
(2)在营救时间最少的前提下,“徐州”舰应按照怎样的航行方向前进?(角度精确到0.1°,时间精确到1min,参考数据:sin68.2°≈0.9286)
【答案】(1)最少需要40min才能靠近商船;(2)前进的方位角约为![]() .
.
【解析】
(1) 由题知舰艇沿直线航行时所需时间最少,设舰艇在B处靠近商船,从A处到靠近商船所用的时间为x h.根据余弦定理,可得![]() ,解方程即得x的值,即得“徐州”舰最少需要多少时间才能靠近商船.(2)由余弦定理可得
,解方程即得x的值,即得“徐州”舰最少需要多少时间才能靠近商船.(2)由余弦定理可得![]() 大小,再求“徐州”舰前进的方位角.
大小,再求“徐州”舰前进的方位角.
(1)由题知舰艇沿直线航行时所需时间最少,设舰艇在B处靠近商船,从A处到靠近商船所用的时间为x h.
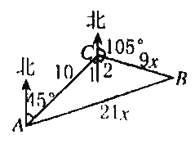
则![]() ,
,![]() ,
,
![]() .
.
又![]() ,
,
根据余弦定理,可得
![]() ,即
,即
![]() ,
,
即![]() ,
,
解得![]() ,
,![]() (舍去).
(舍去).
故“徐州”舰最少需要40min才能靠近商船.
(2)由(1)知![]() ,
,![]() ,
,
由余弦定理可得![]() ,
,
![]() ,
,
故“徐州”舰前进的方位角约为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知集合P的元素个数为![]() 个且元素为正整数,将集合P分成元素个数相同且两两没有公共元素的三个集合A、B、C,即
个且元素为正整数,将集合P分成元素个数相同且两两没有公共元素的三个集合A、B、C,即![]()
![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]()
![]() ,
,![]() ,
,![]()
![]() 若集合A、B、C中的元素满足
若集合A、B、C中的元素满足![]()
![]() ,
,![]() ,
,![]() ,2,
,2,![]() ,则称集合P为“完美集合”.
,则称集合P为“完美集合”.
![]() 若集合
若集合![]() 2,
2,![]() ,
,![]() 2,3,4,5,
2,3,4,5,![]() ,判断集合P和集合Q是否为“完美集合”?并说明理由;
,判断集合P和集合Q是否为“完美集合”?并说明理由;
![]() 已知集合
已知集合![]() x,3,4,5,
x,3,4,5,![]() 为“完美集合”,求正整数x的值;
为“完美集合”,求正整数x的值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() sin2x+
sin2x+ ![]() sin2x.
sin2x.
(1)求函数f(x)的单调递减区间;
(2)在△ABC中,角A,B,C的对边分别为a,b,c,若f( ![]() )=
)= ![]() ,△ABC的面积为3
,△ABC的面积为3 ![]() ,求a的最小值.
,求a的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函f(x)=ax2﹣ex(a∈R). (Ⅰ)a=1时,试判断f(x)的单调性并给予证明;
(Ⅱ)若f(x)有两个极值点x1 , x2(x1<x2).
(i) 求实数a的取值范围;
(ii)证明:﹣ ![]() . (注:e是自然对数的底数)
. (注:e是自然对数的底数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班从6名干部中(其中男生4人,女生2人)选3人参加学校的义务劳动.
(1)设所选3人中女生人数为ξ,求ξ的分布列及Eξ;
(2)求男生甲或女生乙被选中的概率;
(3)在男生甲被选中的情况下,求女生乙也被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 过点
过点![]() ,其参数方程为
,其参数方程为 (
(![]() 为参数,
为参数, ![]() ),以
),以![]() 为极点,
为极点, ![]() 轴非负半轴为极轴,建立极坐标系,曲线
轴非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)求已知曲线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设椭圆 ![]() +
+ ![]() =1(a>b>0)的左右焦点分别为F1 , F2 , 点D在椭圆上,DF1⊥F1F2 ,
=1(a>b>0)的左右焦点分别为F1 , F2 , 点D在椭圆上,DF1⊥F1F2 , ![]() =2
=2 ![]() ,△DF1F2的面积为
,△DF1F2的面积为 ![]() . (Ⅰ)求该椭圆的标准方程;
. (Ⅰ)求该椭圆的标准方程;
(Ⅱ)是否存在圆心在y轴上的圆,使圆在x轴的上方与椭圆有两个交点,且圆在这两个交点处的两条切线互相垂直并分别过不同的焦点?若存在,求出圆的方程;若不存在,请说明理由.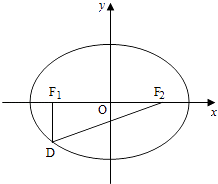
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=(x2﹣2ax)lnx+2ax﹣ ![]() x2 , 其中a∈R.
x2 , 其中a∈R.
(1)若a=0,且曲线f(x)在x=t处的切线l过原点,求直线l的方程;
(2)求f(x)的极值;
(3)若函数f(x)有两个极值点x1 , x2(x1<x2),证明f(x1)+f(x2)< ![]() a2+3a.
a2+3a.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com