
【题目】已知函数f(x)=-x2+2ex+m-1,g(x)=x+![]() (x>0).
(x>0).
(1)若g(x)=m有实根,求m的取值范围;
(2)确定m的取值范围,使得g(x)-f(x)=0有两个相异实根.
【答案】见解析
【解析】
解 (1)∵x>0,∴g(x)=x+![]() ≥2
≥2![]() =2e,
=2e,
等号成立的条件是x=e.
故g(x)的值域是[2e,+∞),因而只需m≥2e,
则g(x)=m就有实根.故m∈[2e,+∞).
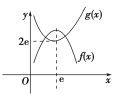
(2)若g(x)-f(x)=0有两个相异的实根,即g(x)=f(x)中函数g(x)与f(x)的图象有两个不同的交点,
作出g(x)=x+![]() (x>0)的大致图象.
(x>0)的大致图象.
∵f(x)=-x2+2ex+m-1=-(x-e)2+m-1+e2.
其对称轴为x=e,开口向下,最大值为m-1+e2.
故当m-1+e2>2e,即m>-e2+2e+1时,
g(x)与f(x)有两个交点,即g(x)-f(x)=0有两个相异实根.
∴m的取值范围是(-e2+2e+1,+∞).


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() ax3-bx2+(2-b)x+1在x=x1处取得极大值,在x=x2处取得极小值,且0<x1<1<x2<2.
ax3-bx2+(2-b)x+1在x=x1处取得极大值,在x=x2处取得极小值,且0<x1<1<x2<2.
(1)证明:a>0;
(2)若z=a+2b,求z的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在[-1,1]上的奇函数f(x),已知当x∈[-1,0]时,f(x)=![]() -
-![]() (a∈R).
(a∈R).
(1)写出f(x)在[0,1]上的解析式;
(2)求f(x)在[0,1]上的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某中学高三文科班学生的数学与地理的水平测试成绩抽样统计如下表:
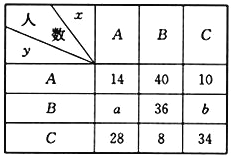
若抽取学生![]() 人,成绩分为
人,成绩分为![]() (优秀),
(优秀),![]() (良好),
(良好),![]() (及格)三个等次,设
(及格)三个等次,设![]() 分别表示数学成绩与地理成绩,例如:表中地理成绩为
分别表示数学成绩与地理成绩,例如:表中地理成绩为![]() 等级的共有
等级的共有![]() (人),数学成绩为
(人),数学成绩为![]() 等级且地理成绩为
等级且地理成绩为![]() 等级的共有8人.已知
等级的共有8人.已知![]() 与
与![]() 均为
均为![]() 等级的概率是
等级的概率是![]() .
.
(1)设在该样本中,数学成绩的优秀率是![]() ,求
,求![]() 的值;
的值;
(2)已知![]() ,
,![]() ,求数学成绩为
,求数学成绩为![]() 等级的人数比
等级的人数比![]() 等级的人数多的概率.
等级的人数多的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果存在函数![]() (
(![]() 为常数),使得对函数
为常数),使得对函数![]() 定义域内任意
定义域内任意![]() 都有
都有![]() 成立,那么称
成立,那么称![]() 为函数
为函数![]() 的一个“线性覆盖函数”.给出如下四个结论:
的一个“线性覆盖函数”.给出如下四个结论:
①函数![]() 存在“线性覆盖函数”;
存在“线性覆盖函数”;
②对于给定的函数![]() ,其“线性覆盖函数”可能不存在,也可能有无数个;
,其“线性覆盖函数”可能不存在,也可能有无数个;
③![]() 为函数
为函数![]() 的一个“线性覆盖函数”;
的一个“线性覆盖函数”;
④若![]() 为函数
为函数![]() 的一个“线性覆盖函数”,则
的一个“线性覆盖函数”,则![]()
其中所有正确结论的序号是___________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.
(1)从袋中随机取出两个球,求取出的球的编号之和不大于4的概率.
(2)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n,求n<m+2的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com