
【题目】如图,三棱柱![]() 中,
中,![]() ,
,![]() 为四边形
为四边形![]() 对角线交点,
对角线交点,![]() 为棱
为棱![]() 的中点,且
的中点,且![]() 平面
平面![]() .
.
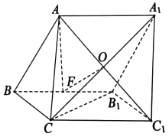
(1)证明:![]() 平面
平面![]() ;
;
(2)证明:四边形![]() 为矩形.
为矩形.
【答案】(1)见解析(2)见解析
【解析】
(1)取![]() 中点
中点![]() ,连结
,连结![]() ,由题意
,由题意![]() 且
且![]() ,证出
,证出![]() ,且
,且![]() ,进而可得
,进而可得![]() ,利用线面平行的判定定理即可证出.
,利用线面平行的判定定理即可证出.
(2)首先证出![]() ,利用线面垂直的性质定理证出
,利用线面垂直的性质定理证出![]() ,再利用线面垂直的判定定理证出
,再利用线面垂直的判定定理证出![]() 平面
平面![]() ,从而可证出
,从而可证出![]() ,根据
,根据![]() ,即证
,即证![]() .
.
证明:(1)取![]() 中点
中点![]() ,连结
,连结![]() .
.

在三棱柱![]() 中,四边形
中,四边形![]() 为平行四边形,
为平行四边形,
![]() 且
且![]() .
.
因为![]() 为平行四边形
为平行四边形![]() 对角线的交点,所以
对角线的交点,所以![]() 为
为![]() 中点,
中点,
又![]() 为
为![]() 中点,所以
中点,所以![]() ,且
,且![]() .
.
又![]() ,
,![]() ,所以
,所以![]() ,且
,且![]() .
.
又![]() 为
为![]() 中点,所以
中点,所以![]() ,且
,且![]() ,
,
所以![]() 为平行四边形,
为平行四边形,
所以![]() ,
,
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() :
:
(2)因为![]() ,
,![]() 为
为![]() 中点,所以
中点,所以![]() ,
,
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() .
.
因为![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
所以![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,所以
,所以![]() ,
,
又由(1)知![]() ,所以
,所以![]() ,
,
在三棱柱![]() 中,四边形
中,四边形![]() 为平行四边形,
为平行四边形,
所以四边形![]() 为矩形.
为矩形.


 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:
【题目】为了研究某学科成绩是否与学生性别有关,采用分层抽样的方法,从高三年级抽取了30名男生和20名女生的该学科成绩,得到如下所示男生成绩的频率分布直方图和女生成绩的茎叶图,规定80分以上为优分(含80分).

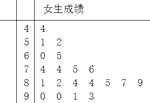
(Ⅰ)(i)请根据图示,将2×2列联表补充完整;
优分 | 非优分 | 总计 | |
男生 | |||
女生 | |||
总计 | 50 |
(ii)据此列联表判断,能否在犯错误概率不超过10%的前提下认为“该学科成绩与性别有关”?
(Ⅱ)将频率视作概率,从高三年级该学科成绩中任意抽取3名学生的成绩,求至少2名学生的成绩为优分的概率.
附:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年春节期间,新型冠状病毒(2019﹣nCoV)疫情牵动每一个中国人的心,危难时刻全国人民众志成城.共克时艰,为疫区助力.我国S省Q市共100家商家及个人为缓解湖北省抗疫消毒物资压力,募捐价值百万的物资对口输送湖北省H市.
(1)现对100家商家抽取5家,其中2家来自A地,3家来自B地,从选中的这5家中,选出3家进行调研.求选出3家中1家来自A地,2家来自B地的概率.
(2)该市一商家考虑增加先进生产技术投入,该商家欲预测先进生产技术投入为49千元的月产增量.现用以往的先进技术投入xi(千元)与月产增量yi(千件)(i=1,2,3,…,8)的数据绘制散点图,由散点图的样本点分布,可以认为样本点集中在曲线![]() 的附近,且:
的附近,且:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其中,
,其中,![]() ,
,![]() ,根据所给的统计量,求y关于x回归方程,并预测先进生产技术投入为49千元时的月产增量.
,根据所给的统计量,求y关于x回归方程,并预测先进生产技术投入为49千元时的月产增量.
附:对于一组数据(u1,v1)(u2,v2),其回归直线v=α+βu的斜率和截距的最小二乘法估计分别为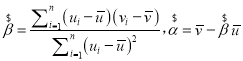
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)求函数![]() 的极值点;
的极值点;
(2)定义:若函数![]() 的图像与直线
的图像与直线![]() 有公共点,我们称函数
有公共点,我们称函数![]() 有不动点.这里取:
有不动点.这里取:![]() ,若
,若![]() ,如果函数
,如果函数![]() 存在不动点,求实数
存在不动点,求实数![]() 取值范围.
取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行元旦促销回馈活动,凡购物满1000元,即可参与抽奖活动,抽奖规则如下:在一个不透明的口袋中装有编号为1、2、3、4、5的5个完全相同的小球,顾客每次从口袋中摸出一个小球,共摸三次(每次摸出的小球均不放回口袋),编号依次作为一个三位数的个位、十位、百位,若三位数是奇数,则奖励50元,若三位数是偶数,则奖励![]() 元(
元(![]() 为三位数的百位上的数字,如三位数为234,则奖励
为三位数的百位上的数字,如三位数为234,则奖励![]() 元).
元).
(1)求抽奖者在一次抽奖中所得三位数是奇数的概率;
(2)求抽奖者在一次抽奖中获奖金额![]() 的概率分布与期望
的概率分布与期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1为某省2018年1~4月快递业务量统计图,图2是该省2018年1~4月快递业务收入统计图,下列对统计图理解错误的是( )


A. 2018年1~4月的业务量,3月最高,2月最低,差值接近2000万件
B. 2018年1~4月的业务量同比增长率均超过50%,在3月底最高
C. 从两图来看,2018年1~4月中的同一个月的快递业务量与收入的同比增长率并不完全一致
D. 从1~4月来看,该省在2018年快递业务收入同比增长率逐月增长
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为支援武汉抗击新冠肺炎疫情,军队抽组1400名医护人员于2月3日起承担武汉火神山专科医院医疗救治任务.此外,从解放军疾病预防控制中心、军事科学院军事医学研究院抽取15名专家组成联合专家组,指导医院疫情防控工作.该医院开设了重症监护病区(![]() ),重症病区(
),重症病区(![]() ),普通病区(
),普通病区(![]() )三个病区.现在将甲乙丙丁4名专家分配到这三个病区了解情况,要求每个专家去一个病区,每个病区都有专家,一个病区可以有多个专家.已知甲不能去重症监护病区(
)三个病区.现在将甲乙丙丁4名专家分配到这三个病区了解情况,要求每个专家去一个病区,每个病区都有专家,一个病区可以有多个专家.已知甲不能去重症监护病区(![]() ),乙不能去重症病区(
),乙不能去重症病区(![]() ),则一共有__________种分配方式
),则一共有__________种分配方式
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com