
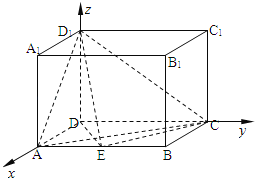
【题目】如图,长方体ABCD﹣A1B1C1D1中,AD=AA1=1,AB=2,点E是线段AB中点.

(1)证明:D1E⊥CE;
(2)求二面角D1﹣EC﹣D的大小的余弦值;
(3)求A点到平面CD1E的距离.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据线面垂直的性质定理,证明CE⊥面D1DE即可证明:D1E⊥CE;
(2)建立坐标系,利用向量法即可求二面角D1﹣EC﹣D的大小的余弦值;
(3)根据点到平面的距离公式,即可求A点到平面CD1E的距离.
(1)证明:DD1⊥面ABCD,CE面ABCD;
所以DD1⊥CE,
Rt△DAE中,AD=1,AE=1,
DE![]() ,
,
同理:CE![]() ,又CD=2,CD2=CE2+DE2,
,又CD=2,CD2=CE2+DE2,
DE⊥CE,
DE∩CE=E,
所以,CE⊥面D1DE,
又D1E面D1EC,
所以,D1E⊥CE;
(2)设平面CD1E的法向量为![]() (x,y,z),
(x,y,z),
由(1)得![]() (1,1,﹣1),
(1,1,﹣1),![]() (1,﹣1,0)
(1,﹣1,0)
![]()
![]() x+y﹣1=0,
x+y﹣1=0,![]()
![]() x﹣y=0
x﹣y=0
解得:x=y![]() ,即
,即![]() (
(![]() ,
,![]() ,1);
,1);
又平面CDE的法向量为![]() (0,0,1),
(0,0,1),
∴cos![]() ,
,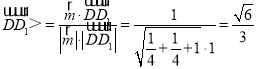 span>,
span>,
所以,二面角D1﹣EC﹣D的余弦值为![]() ;
;
(3)由(1)(2)知![]() (0,1,0),平面CD1E的法向量为
(0,1,0),平面CD1E的法向量为![]() (
(![]() ,
,![]() ,1);
,1);
故A点到平面CD1E的距离为d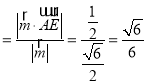 .
.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中数学 来源: 题型:
【题目】某市有两家共享单车公司,在市场上分别投放了黄、蓝两种颜色的单车,已知黄、蓝两种颜色的单车的投放比例为2:1.监管部门为了了解两种颜色的单车的质量,决定从市场中随机抽取5辆单车进行体验,若每辆单车被抽取的可能性相同.
(1)求抽取的5辆单车中有2辆是蓝色颜色单车的概率;
(2)在骑行体验过程中,发现蓝色单车存在一定质量问题,监管部门决定从市场中随机地抽取一辆送技术部门作进一步抽样检测,并规定若抽到的是蓝色单车,则抽样结束,若抽取的是黄色单车,则将其放回市场中,并继续从市场中随机地抽取下一辆单车,并规定抽样的次数最多不超过![]() (
(![]() )次.在抽样结束时,已取到的黄色单车以
)次.在抽样结束时,已取到的黄色单车以![]() 表示,求
表示,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 、
、![]() 是异面直线,给出下列结论:
是异面直线,给出下列结论:
①一定存在平面![]() ,使直线
,使直线![]() 平面
平面![]() ,直线
,直线![]() 平面
平面![]() ;
;
②一定存在平面![]() ,使直线
,使直线![]() 平面
平面![]() ,直线
,直线![]() 平面
平面![]() ;
;
③一定存在无数个平面![]() ,使直线
,使直线![]() 与平面
与平面![]() 交于一个定点,且直线
交于一个定点,且直线![]() 平面
平面![]() .
.
则所有正确结论的序号为( )
A.①②B.②C.②③D.③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,过
,过![]() 作垂直于
作垂直于![]() 轴的直线交该椭圆于
轴的直线交该椭圆于![]() ,
,![]() 两点,直线
两点,直线![]() 的斜率为
的斜率为![]() .
.
(Ⅰ)求椭圆的离心率;
(Ⅱ)若![]() 的外接圆在
的外接圆在![]() 处的切线与椭圆交另一点于
处的切线与椭圆交另一点于![]() ,且
,且![]() 的面积为
的面积为![]() ,求椭圆的方程.
,求椭圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】保护环境,防治环境污染越来越得到人们的重视,某企业在现有设备下每日生产总成本![]() (单位:万元)与日产量
(单位:万元)与日产量![]() (单位:吨)之间的函数关系式为
(单位:吨)之间的函数关系式为![]() .现为了减少大气污染,该企业引进了除尘设备,每吨产品除尘费用为
.现为了减少大气污染,该企业引进了除尘设备,每吨产品除尘费用为![]() 万元,除尘后,当日产量
万元,除尘后,当日产量![]() 时,每日生产总成本
时,每日生产总成本![]() .
.
(1)求![]() 的值;
的值;
(2)若每吨产品出厂价为48万元,试求除尘后日产量为多少吨时,每吨产品的利润最大,最大利润为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
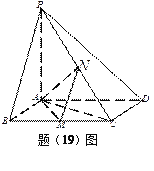
【题目】(本小题满分12分)
如图,已知四棱锥![]() ,底面
,底面![]() 为菱形,
为菱形,![]() ,
,
![]() ,
, ![]() 平面
平面![]() ,
, ![]() 分别是
分别是![]() 的中点。
的中点。
(1)证明: ![]() ;
;
(2)若![]() 为
为![]() 上的动点,
上的动点,![]() 与平面
与平面![]() 所成最大角
所成最大角
的正切值为![]() ,求二面角
,求二面角![]() 的余弦值。
的余弦值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com