
【题目】某一电视台对年龄高于40岁和不高于40岁的人是否喜欢西班牙队进行调查,40岁以上调查了50人,不高于40岁调查了50人,所得数据制成如下列联表:
不喜欢西班牙队 | 喜欢西班牙队 | 总计 | |
40岁以上 |
|
| 50 |
不高于40岁 | 15 | 35 | 50 |
总计 |
|
| 100 |
已知工作人员从所有统计结果中任取一个,取到喜欢西班牙队的人的概率为![]() ,则有超过________的把握认为年龄与西班牙队的被喜欢程度有关.
,则有超过________的把握认为年龄与西班牙队的被喜欢程度有关.
参考公式与临界值表:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.702 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
科目:高中数学 来源: 题型:
【题目】如图所示,在直三棱柱![]() 中,
中,![]() ,
,![]() 平面
平面![]() ,D为AC的中点.
,D为AC的中点.
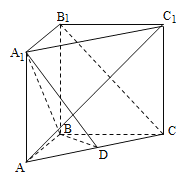
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() 平面
平面![]() ;
;
(3)设E是![]() 上一点,试确定E的位置使平面
上一点,试确定E的位置使平面![]() 平面BDE,并说明理由.
平面BDE,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方形ABCD的边长为7,点M在AB上,点N在BC上,且AM=BN=3,现有一束光线从点M射向点N,光线每次碰到正方形的边时反射,则这束光线从第一次回到原点M时所走过的路程为( )
A. ![]() B. 60 C.
B. 60 C. ![]() D. 70
D. 70
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过抛物线![]() 的焦点
的焦点![]() 的直线与抛物线交于
的直线与抛物线交于![]() 两点,且
两点,且![]() ,抛物线的准线
,抛物线的准线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 于点
于点![]() ,且四边形
,且四边形![]() 的面积为
的面积为![]() ,过
,过![]() 的直线
的直线![]() 交抛物线于
交抛物线于![]() 两点,且
两点,且![]() ,点
,点![]() 为线段
为线段![]() 的垂直平分线与
的垂直平分线与![]() 轴的交点,则点
轴的交点,则点![]() 的横坐标
的横坐标![]() 的取值范围为( )
的取值范围为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于![]() 的函数
的函数![]() ,
,
(I)试求函数![]() 的单调区间;
的单调区间;
(II)若![]() 在区间
在区间![]() 内有极值,试求a的取值范围;
内有极值,试求a的取值范围;
(III)![]() 时,若
时,若![]() 有唯一的零点
有唯一的零点![]() ,试求
,试求![]() .(注:
.(注:![]() 为取整函数,表示不超过
为取整函数,表示不超过![]() 的最大整数,如
的最大整数,如![]() ;以下数据供参考:
;以下数据供参考:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题:(1)若![]() ,
,![]() 为非零向量且
为非零向量且![]() ,则
,则![]() ;(2)已知向量
;(2)已知向量![]() ,
,![]() ,若
,若![]() ,则
,则![]() ;(3)若
;(3)若![]() ,
,![]() ,
,![]() 为单位向量,且
为单位向量,且![]() ,则三角形
,则三角形![]() 为等边三角形;其中正确的个数是( )
为等边三角形;其中正确的个数是( )
A.1B.2C.3D.0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() :
:![]() 与抛物线
与抛物线![]() 切于点
切于点![]() ,直线
,直线![]() :
:![]() 过定点Q,且抛物线
过定点Q,且抛物线![]() 上的点到点Q的距离与其到准线距离之和的最小值为
上的点到点Q的距离与其到准线距离之和的最小值为![]() .
.
(1)求抛物线![]() 的方程及点
的方程及点![]() 的坐标;
的坐标;
(2)设直线![]() 与抛物线
与抛物线![]() 交于(异于点P)两个不同的点A、B,直线PA,PB的斜率分别为
交于(异于点P)两个不同的点A、B,直线PA,PB的斜率分别为![]() ,那么是否存在实数
,那么是否存在实数![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1:x+2y+1=0,l2:-2x+y+2=0,它们相交于点A.
(1)判断直线l1和l2是否垂直?请给出理由.
(2)求过点A且与直线l3:3x+y+4=0平行的直线方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com