
【题目】如图所示多面体中,AD⊥平面PDC,四边形ABCD为平行四边形,点E,F分别为AD,BP的中点,AD=3,AP=3![]() ,PC
,PC![]() .
.
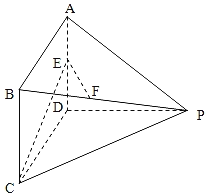
(1)求证:EF//平面PDC;
(2)若∠CDP=120°,求二面角E﹣CP﹣D的平面角的余弦值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)取![]() 的中点为
的中点为![]() ,连结
,连结![]() ,
,![]() ,四边形
,四边形![]() 是平行四边形,
是平行四边形,![]() ,
,![]() 平面
平面![]() .
.
(2)由余弦定理求出![]() ,以
,以![]() 为原点,在平面
为原点,在平面![]() 内过
内过![]() 作
作![]() 的垂线为
的垂线为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立空间直角坐标系,利用向量法能求出二面角
轴,建立空间直角坐标系,利用向量法能求出二面角![]() 的平面角的余弦值.
的平面角的余弦值.
解:(1)证明:取![]() 的中点为
的中点为![]() ,连结
,连结![]() ,
,![]() ,
,
![]() ,
,![]() 分别为
分别为![]() 、
、![]() 的中点,
的中点,
![]() ,且
,且![]() ,
,
又四边形![]() 为平行四边形,
为平行四边形,![]() ,且
,且![]() ,
,
![]() ,且
,且![]() ,
,![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.
(2)![]() 平面
平面![]() ,四边形
,四边形![]() 为平行四边形,
为平行四边形,
点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,![]() ,
,![]() ,
,
![]() .
.![]() ,
,
![]() ,解得
,解得![]() ,
,
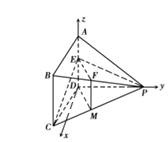
如图,以![]() 为原点,在平面
为原点,在平面![]() 内过
内过![]() 作
作![]() 的垂线为
的垂线为![]() 轴,
轴,
![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,
则![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
设平面![]() 的一个法向量
的一个法向量![]() ,
,
![]() ,4,
,4,![]() ,
,![]() ,3,
,3,![]() ,
,
则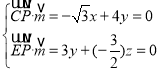 ,取
,取![]() ,得
,得![]() ,
,
平面![]() 的一个法向量
的一个法向量![]() ,
,
设二面角![]() 的平面角为
的平面角为![]() ,
,
则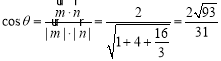 .
.
![]() 二面角
二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】某同学在微信上查询到近十年全国高考报名人数、录取人数和山东夏季高考报名人数的折线图,其中![]() 年的录取人数被遮挡了.他又查询到近十年全国高考录取率的散点图,结合图表中的信息判定下列说法正确的是( )
年的录取人数被遮挡了.他又查询到近十年全国高考录取率的散点图,结合图表中的信息判定下列说法正确的是( )

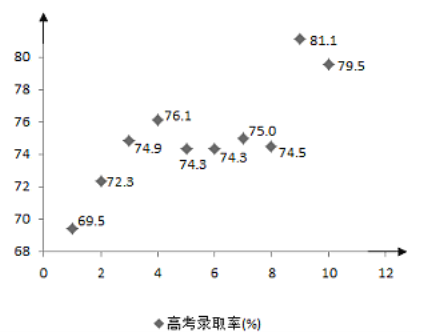
A.全国高考报名人数逐年增加
B.![]() 年全国高考录取率最高
年全国高考录取率最高
C.![]() 年高考录取人数约
年高考录取人数约![]() 万
万
D.![]() 年山东高考报名人数在全国的占比最小
年山东高考报名人数在全国的占比最小
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为F,直线l与C交于M,N两点.
的右焦点为F,直线l与C交于M,N两点.
(1)若l过点F,点M,N到直线y=2的距离分别为d1,d2,且![]() ,求l的方程;
,求l的方程;
(2)若点M的坐标为(0,1),直线m过点M交C于另一点N′,当直线l与m的斜率之和为2时,证明:直线NN′过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 在椭圆
在椭圆![]() :
: ![]() 上,
上, ![]() 是椭圆的一个焦点.
是椭圆的一个焦点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)椭圆C上不与![]() 点重合的两点
点重合的两点![]() ,
, ![]() 关于原点O对称,直线
关于原点O对称,直线![]() ,
, ![]() 分别交
分别交![]() 轴于
轴于![]() ,
, ![]() 两点.求证:以
两点.求证:以![]() 为直径的圆被直线
为直径的圆被直线![]() 截得的弦长是定值.
截得的弦长是定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了打击海盗犯罪,甲、乙、丙三国海军进行联合军事演习,分别派出一艘军舰A,B,C.演习要求:任何时刻军舰A、B、C均不得在同一条直线上.
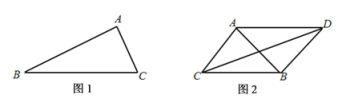
(1)如图1,若演习过程中,A、B间的距离始终保持![]() ,B,C间的距离始终保持
,B,C间的距离始终保持![]() ,求
,求![]() 的最大值.
的最大值.
(2)如图2,若演习过程中,A,C间的距离始终保持![]() ,B、C间的距离始终保持
,B、C间的距离始终保持![]() .且当
.且当![]() 变化时,模拟海盗船D始终保持:到B的距离与A、B间的距离相等,
变化时,模拟海盗船D始终保持:到B的距离与A、B间的距离相等,![]() ,与C在直线AB的两侧,求C与D间的最大距离.
,与C在直线AB的两侧,求C与D间的最大距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】极坐标系中椭圆C的方程为![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴非负半轴,建立平面直角坐标系,且两坐标系取相同的单位长度.
轴非负半轴,建立平面直角坐标系,且两坐标系取相同的单位长度.
(Ⅰ)求该椭圆的直角标方程,若椭圆上任一点坐标为![]() ,求
,求![]() 的取值范围;
的取值范围;
(Ⅱ)若椭圆的两条弦![]() ,
,![]() 交于点
交于点![]() ,且直线
,且直线![]() 与
与![]() 的倾斜角互补,求证:
的倾斜角互补,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校高三年级在开学时举行了入学检测.为了了解本年级学生寒假期间历史的学习情况,现从年级![]() 名文科生中随机抽取了
名文科生中随机抽取了![]() 名学生本次考试的历史成绩,得到他们历史分数的频率分布直方图如图.已知本次考试高三年级历史成绩分布区间为
名学生本次考试的历史成绩,得到他们历史分数的频率分布直方图如图.已知本次考试高三年级历史成绩分布区间为![]() .
.

(1)求图中![]() 的值;
的值;
(2)根据频率分布直方图,估计这![]() 名学生历史成绩的平均分,众数;(每组数据用该组的区间中点值作代表)
名学生历史成绩的平均分,众数;(每组数据用该组的区间中点值作代表)
(3)已知该学校每年高考有![]() %的同学历史成绩在一本线以上,用样本估计总体的方法,请你估计本次入学检测历史学科划定的一本线该为多少分?
%的同学历史成绩在一本线以上,用样本估计总体的方法,请你估计本次入学检测历史学科划定的一本线该为多少分?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com