
【题目】已知函数![]() ,其中
,其中![]() 为自然对数的底数,常数
为自然对数的底数,常数![]() .
.
(1)求函数![]() 在区间
在区间![]() 上的零点个数;
上的零点个数;
(2)函数![]() 的导数
的导数![]() ,是否存在无数个
,是否存在无数个![]() ,使得
,使得![]() 为函数
为函数![]() 的极大值点?说明理由.
的极大值点?说明理由.
【答案】(1)1(2)存在
【解析】【试题分析】(1)对函数求导后得到函数的单调区间,利用二分法判断函数在给定区间上只有一个零点.(2)原命题等价于,存在无数个![]() ,使得
,使得![]() 成立,求得
成立,求得![]() 的表达式,构造为函数
的表达式,构造为函数![]() ,利用导数证得
,利用导数证得![]() 存在负值即可.
存在负值即可.
【试题解析】
(1)![]() ,当
,当![]() 时,
时, ![]() 单调递减;当
单调递减;当![]() 时,
时, ![]() 单调递增;
单调递增;
因为![]() ,所以存在
,所以存在![]() ,使
,使![]() ,
,
且当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() .
.
故函数![]() 在区间
在区间![]() 上有1个零点,即
上有1个零点,即![]() .
.
(2)(法一)当![]() 时,
时, ![]() .
.
因为当![]() 时,
时, ![]() ;当
;当![]() ,
, ![]() .
.
由(1)知,当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
下证:当![]() 时,
时, ![]() ,即证
,即证![]() .
.
![]() ,
,
记![]() …
…
![]() ,所以
,所以![]() 在
在![]() 单调递增,
单调递增,
由![]() ,
,
所以存在唯一零点![]() ,使得
,使得![]() ,且
,且![]() 时,
时, ![]() 单调递减,
单调递减,
![]() 时,
时, ![]() 单调递增.
单调递增.
所以当![]() 时,
时, ![]() .……
.……
由![]() ,得当
,得当![]() 时,
时, ![]() .
.
故![]() .
.
当![]() 时,
时, ![]() 单调递增;
单调递增;
当![]() 时,
时, ![]() 单调递减.
单调递减.
所以存在![]() ,使得
,使得![]() 为
为![]() 的极大值点.
的极大值点.
(2)(法二)因为当![]() 时,
时, ![]() ;当
;当![]() ,
, ![]() .
.
由(1)知,当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() .
.
所以存在无数个![]() ,使得
,使得![]() 为函数
为函数![]() 的极大值点,即存在无数个
的极大值点,即存在无数个![]() ,使得
,使得![]() 成立, ①…由(1),问题①等价于,存在无数个
成立, ①…由(1),问题①等价于,存在无数个![]() ,使得
,使得![]() 成立,
成立,
因为![]() ,
,
记![]() …
…
![]() 因为
因为![]() ,当
,当![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 单调递增,因为
单调递增,因为![]() ,
,
所以存在唯一零点![]() ,使得
,使得![]() ,且当
,且当![]() 时,
时, ![]() 单调递减;当
单调递减;当![]() 时,
时, ![]() 单调递增;
单调递增;
所以,当![]() 时,
时, ![]() , ②…
, ②…
由![]() ,可得
,可得![]() ,代入②式可得
,代入②式可得![]() ,
,
当![]() 时,
时, ![]() ,
,
所以,必存在![]() ,使得
,使得![]() ,即对任意
,即对任意![]() 有解,
有解,
所以对任意![]() ,函数
,函数![]() 存在极大值点为
存在极大值点为![]() .…
.…


科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程是
的参数方程是 (
(![]() 为参数),以该直角坐标系的原点
为参数),以该直角坐标系的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有甲、乙两个桔柚(球形水果)种植基地,已知所有采摘的桔柚的直径都在![]() 范围内(单位:毫米,以下同),按规定直径在
范围内(单位:毫米,以下同),按规定直径在![]() 内为优质品,现从甲、乙两基地所采摘的桔柚中各随机抽取500个,测量这些桔柚的直径,所得数据整理如下:
内为优质品,现从甲、乙两基地所采摘的桔柚中各随机抽取500个,测量这些桔柚的直径,所得数据整理如下:

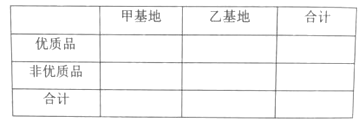
(1)根据以上统计数据完成下面![]() 列联表,并回答是否有
列联表,并回答是否有![]() 以上的把握认为“桔柚直径与所在基地有关”?
以上的把握认为“桔柚直径与所在基地有关”?
(2)求优质品率较高的基地的500个桔柚直径的样本平均数![]() (同一组数据用该区间的中点值作代表);
(同一组数据用该区间的中点值作代表);
(3)记甲基地直径在![]() 范围内的五个桔柚分别为
范围内的五个桔柚分别为![]() ,现从中任取二个,求含桔柚
,现从中任取二个,求含桔柚![]() 的概率.
的概率.
附: 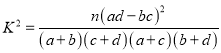 ,
, ![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,且点
,且点![]() 到椭圆
到椭圆![]() 上任意一点的最大距离为3,椭圆
上任意一点的最大距离为3,椭圆![]() 的离心率为
的离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)是否存在斜率为![]() 的直线
的直线![]() 与以线段
与以线段![]() 为直径的圆相交于
为直径的圆相交于![]() 、
、![]() 两点,与椭圆相交于
两点,与椭圆相交于![]() 、
、![]() ,且
,且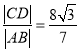 ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中, PA⊥平面ABCD,E为BD的中点,G为PD的中点,△DAB≌△DCB,EA=EB=AB=1, ![]() ,连接CE并延长交AD于F.
,连接CE并延长交AD于F.
(Ⅰ)求证:AD⊥CG;
(Ⅱ)求平面BCP与平面DCP的夹角的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为抛物线
为抛物线![]() 的焦点,点
的焦点,点![]() 为其上一点,
为其上一点,![]() 与
与![]() 关于
关于![]() 轴对称,直线
轴对称,直线![]() 与抛物线交于异于
与抛物线交于异于![]() 的
的![]() 两点,
两点,![]() ,
,![]() .
.
(1)求抛物线的标准方程和![]() 点的坐标;
点的坐标;
(2)判断是否存在这样的直线![]() ,使得
,使得![]() 的面积最小.若存在,求出直线
的面积最小.若存在,求出直线![]() 的方程和
的方程和![]() 面积的最小值;若不存在,请说明理由.
面积的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量分别在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:克)中,经统计得频率分布直方图如图所示.
(单位:克)中,经统计得频率分布直方图如图所示.

(1)现按分层抽样从质量为![]() ,
,![]() 的芒果中随机抽取
的芒果中随机抽取![]() 个,再从这
个,再从这![]() 个中随机抽取
个中随机抽取![]() 个,记随机变量
个,记随机变量![]() 表示质量在
表示质量在![]() 内的芒果个数,求
内的芒果个数,求![]() 的分布列及数学期望.
的分布列及数学期望.
(2)以各组数据的中间数代表这组数据的平均值,将频率视为概率,某经销商来收购芒果,该种植园中还未摘下的芒果大约还有![]() 个,经销商提出如下两种收购方案:
个,经销商提出如下两种收购方案:
A:所以芒果以![]() 元/千克收购;
元/千克收购;
B:对质量低于![]() 克的芒果以
克的芒果以![]() 元/个收购,高于或等于
元/个收购,高于或等于![]() 克的以
克的以![]() 元/个收购.
元/个收购.
通过计算确定种植园选择哪种方案获利更多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年6月深圳地铁总公司对深圳地铁1号线30个站的工作人员的服务态度进行了满意度调查,其中世界之窗、白石洲、高新园、深大、桃园、大新6个站的得分情况如下:
地铁站 | 世界之窗 | 白石州 | 高新园 | 深大 | 桃园 | 大新 |
满意度得分 | 70 | 76 | 72 | 70 | 72 | x |
已知6个站的平均得分为75分.
(1)求大新站的满意度得分x,及这6个站满意度得分的标准差;
(2)从表中前5个站中,随机地选2个站,求恰有1个站得分在区间(68,75)中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程是:
的参数方程是: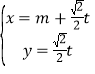 (
(![]() 是参数,
是参数,![]() 是常数).以
是常数).以![]() 为极点,
为极点,![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 、
、![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com