
【题目】若 ![]() 则下列结论正确的是( )
则下列结论正确的是( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】C
【解析】函数y=5x在R上是增函数,∵1.2<0,∴51.2<50=1.又∵51.2>0,∴0<51.2<1,即0<a<1.
函数y=1.2x在R上是增函数,∵1.1>0,∴1.21.1>1.20.∴1.21.1>1,即b>1.
函数y=lgx在(0,+∞),上是增函数,∵ ![]() ,∴
,∴ ![]() ,∴
,∴ ![]() ,即c<0.∴c<a<b,∴A,B不正确;
,即c<0.∴c<a<b,∴A,B不正确;
∵0<a<1,∴lna<0,∵ ![]() ,∴
,∴ ![]() .∴C正确;∵0<a<1,∴30<3a<31,即1<3a<3,
.∴C正确;∵0<a<1,∴30<3a<31,即1<3a<3,
∵b>1,∴ ![]() .∴
.∴ ![]() .∴
.∴ ![]() .∴D不正确。∴结论正确的是:C.
.∴D不正确。∴结论正确的是:C.
所以答案是:C.
【考点精析】根据题目的已知条件,利用指数函数的单调性与特殊点和对数函数的单调性与特殊点的相关知识可以得到问题的答案,需要掌握0<a<1时:在定义域上是单调减函数;a>1时:在定义域上是单调增函数;过定点(1,0),即x=1时,y=0;a>1时在(0,+∞)上是增函数;0>a>1时在(0,+∞)上是减函数.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 为正整数,数列
为正整数,数列![]() 满足
满足![]() ,
, ![]() ,设数列
,设数列![]() 满足
满足![]()
(1)求证:数列![]() 为等比数列;
为等比数列;
(2)若数列![]() 是等差数列,求实数
是等差数列,求实数![]() 的值;
的值;
(3)若数列![]() 是等差数列,前
是等差数列,前![]() 项和为
项和为![]() ,对任意的
,对任意的![]() ,均存在
,均存在![]() ,使得
,使得![]() 成立,求满足条件的所有整数
成立,求满足条件的所有整数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018海南高三阶段性测试(二模)】如图,在直三棱柱![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 上一动点.
上一动点.
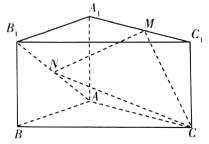
(I)是否存在一点![]() ,使得线段
,使得线段![]() 平面
平面![]() ?若存在,指出点
?若存在,指出点![]() 的位置,若不存在,请说明理由.
的位置,若不存在,请说明理由.
(II)若点![]() 为
为![]() 的中点且
的中点且![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 在一个特定时段内,以点E为中心的7海里以内海域被设为警戒水域.点E正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船只位于点A北偏东![]() 且与点A相距40
且与点A相距40![]() 海里的位置B,经过40分钟又测得该船已行驶到点A北偏东
海里的位置B,经过40分钟又测得该船已行驶到点A北偏东![]() +
+![]() (其中sin
(其中sin![]() =
=![]() ,
,![]() )且与点A相距10
)且与点A相距10![]() 海里的位置C.
海里的位置C.
(I)求该船的行驶速度(单位:海里/小时);
(II)若该船不改变航行方向继续行驶.判断它是否会进入警戒水域,并说明理由.


查看答案和解析>>
科目:高中数学 来源: 题型:
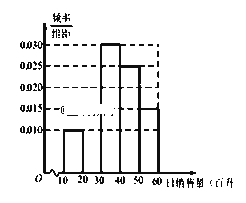
【题目】某加油站20名员工日销售量的频率分布直方图,如图所示:
(1)补全该频率分布直方图在[20,30)的部分,并分别计算日销售量在 [10,20),[20,30)的员工数;
(2)在日销量为[10,30)的员工中随机抽取2人,求这两名员工日销量在 [20,30)的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子中装有5张编号依次为1、2、3、4、5的卡片,这5 张卡片除号码外完全相同.现进行有放回的连续抽取2 次,每次任意地取出一张卡片.
(1)求出所有可能结果数,并列出所有可能结果;
(2)求事件“取出卡片号码之和不小于7 或小于5”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校举办校园科技文化艺术节,在同一时间安排《生活趣味数学》和《校园舞蹈赏析》两场讲座.已知A、B两学习小组各有5位同学,每位同学在两场讲座任意选听一场.若A组1人选听《生活趣味数学》,其余4人选听《校园舞蹈赏析》;B组2人选听《生活趣味数学》,其余3人选听《校园舞蹈赏析》.
(1)若从此10人中任意选出3人,求选出的3人中恰有2人选听《校园舞蹈赏析》的概率;
(2)若从A、B两组中各任选2人,设X为选出的4人中选听《生活趣味数学》的人数,求X的分布列和数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱柱ABCD﹣A1B1C1D1中,底面ABCD为菱形,AA1⊥底面ABCD,E为B1D的中点. 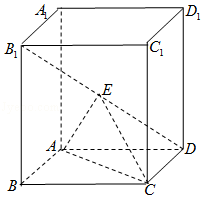
(Ⅰ)证明:平面ACE⊥平面ABCD;
(Ⅱ)若二面角D﹣AE﹣C为60°,AA1=AB=1,求三棱锥C﹣AED的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com