Question

【题目】学校有线网络同时提供A、B两套校本选修课程。A套选修课播40分钟，课后研讨20分钟，可获得学分5分B套选修课播32分钟，课后研讨40分钟，可获学分4分。全学期20周，网络每周开播两次，每次均为独立内容。学校规定学生每学期收看选修课不超过1400分钟，研讨时间不得少于1000分钟。两套选修课怎样合理选择，才能获得最好学分成绩？

Answer 1

【答案】答案见解析.

【解析】试题分析：设选择两套课程分别为次， 为学分，根据两套选修课所得学分可得目标函数，根据学校规定学生每学期收看选修课不超过分钟，研讨时间不得少于分钟及为正数，可得表示约束条件的二元一次不等式组，画出可行域，平移目标函数所表示的直线，结合最优解为整数点，可得最优解，从而可得结果.

试题解析：设选择A、B两套课程分别为X、Y次，z为学分，

则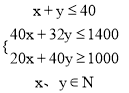 目标函数

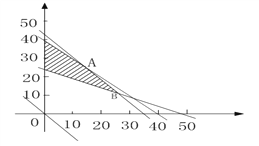
由方程组解得点A(15,25) , B(25,12.5)

由于目标函数的斜率与直线AB的斜率相等，因此在图中阴影线段AB上的整数点A（15，25）、C（19，20）、D（23，15）都符合题意，使得学分最高为175分。