
分析 (Ⅰ)由题意可知:准线l的方程为:y=-$\frac{p}{2}$,准线l圆x2+y2=4相切,则$\frac{p}{2}$=2,解得:p=4,即可求得抛物线C的方程;
(Ⅱ)设直线m:y=kx+1,代入抛物线方程由韦达定理可知:x1•x2=-8,y1•y2=(kx1+1)(kx2+1)=-8k2+8k+1,根据向量数量积的坐标运算,即可求得 $\overrightarrow{OA}$•$\overrightarrow{OB}$=x1•x2+y1•y2=-7.
解答 解:(Ⅰ)依题意,可设抛物线C的方程为:x2=2py,p>0
其准线l的方程为:y=-$\frac{p}{2}$,
∵准线l圆x2+y2=4相切,
∴$\frac{p}{2}$=2,解得:p=4,
故抛物线线C的方程为:x2=8y;….…(5分)
(Ⅱ)命题p为真命题 …(6分)
证明:直线m和抛物线C交于A,B且过定点(0,1),
故所以直线m的斜率k一定存在,…(7分)
设直线m:y=kx+1,交点A(x1,y1)B(x2,y2).
联立抛物线C的方程,$\left\{\begin{array}{l}{y=kx+1}\\{{x}^{2}=8y}\end{array}\right.$
整理得:x2-8kx-8=0,△=64k2+64>0恒成立,…(8分)
由韦达定理得:x1+x2=8k,x1•x2=-8,…(9分)
y1•y2=(kx1+1)(kx2+1)=k2x1•x2+k(x1+x2)+1=-8k2+8k+1
$\overrightarrow{OA}$•$\overrightarrow{OB}$=x1•x2+y1•y2=-8+-8k2+8k+1=-7,
∴命题P为真命题.…(12分).
点评 本题考查抛物线的标准方程及性质,考查点到直线的距离公式,直线与抛物线的位置关系,向量数量积的坐标运算,考查计算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,+∞) | B. | [2,+∞) | C. | [$\frac{1}{2}$,+∞) | D. | [$\frac{1}{2}$,$\frac{5}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | z的实部为-$\frac{1}{2}$ | B. | z的虚部为-$\frac{1}{2}$i | ||
| C. | |z|=$\frac{1}{2}$ | D. | z的共轭复数为$\frac{1}{2}$+$\frac{1}{2}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
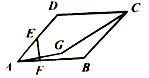 如图所示,四边形ABCD是菱形,边长为2,∠BAD=60°,E为边AD的中点,点F在边AB上运动,点A关于直线EF的对称点为G,则线段CG的长度最小值为( )
如图所示,四边形ABCD是菱形,边长为2,∠BAD=60°,E为边AD的中点,点F在边AB上运动,点A关于直线EF的对称点为G,则线段CG的长度最小值为( )| A. | $\sqrt{7}-1$ | B. | 2 | C. | $\sqrt{5}-1$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 45 | B. | 46 | C. | 47 | D. | 48 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | $\sqrt{3}$+2 | D. | $2\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com