
【题目】某租赁公司拥有汽车100辆.当每辆车的月租金为3 000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.
(1)当每辆车的月租金定为3 600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
【答案】(1) 88(2)当每辆车的月租金定为4 050元时,月收益最大,其值为307 050元
【解析】
试题分析:(1)当每辆车的月租金为x元时,租出的车辆100-![]() (辆),把x=3600代入计算;
(辆),把x=3600代入计算;
(2)设每辆车的月租金为x元,租赁公司的月收益函数y,建立函数解析式,求出最大值即可
试题解析:(1)当每辆车的月租金定为3 600元时,未租出的车辆数为![]() =12,所以这时租出了100-12=88辆车.
=12,所以这时租出了100-12=88辆车.
(2)设每辆车的月租金定为x元,则租赁公司的月收益为
f(x)=![]() (x-150)-
(x-150)-![]() ×50=-
×50=-![]() (x-4 050)2+307 050.
(x-4 050)2+307 050.
所以,当x=4 050 时,f(x)最大,其最大值为f(4 050)=307 050.
当每辆车的月租金定为4 050元时,月收益最大,其值为307 050元.


科目:高中数学 来源: 题型:
【题目】从某居民区随机抽取10个家庭,获得第i个家庭的月收入xi(单位:千元)与月储蓄yi(单位:千元)的数据资料,算得![]() =80,
=80, ![]() =20,
=20, ![]() =184,
=184, ![]() =720.
=720.
(Ⅰ)求家庭的月储蓄y对月收入x的线性回归方程y=bx+a;
(Ⅱ)判断变量x与y之间是正相关还是负相关;
(Ⅲ)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中日“钓鱼岛争端”问题越来越引起社会关注,我校对高一![]() 名学生进行了一次“钓鱼岛”知识测试,并从中抽取了部分学生的成绩,(满分
名学生进行了一次“钓鱼岛”知识测试,并从中抽取了部分学生的成绩,(满分![]() 分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.
分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.
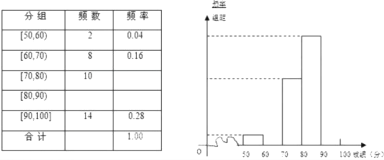
(1)填写答题卡频率分布表中的空格, 补全频率分布直方图, 并标出每个小矩形对应的纵轴数据;
(2)请你估算该年级的平均数及中位数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个几何体的三视图如图所示,已知正(主)视图是底边长为1的平行四边形,侧(左)视图是一个长为![]() ,宽为1的矩形,俯视图为两个边长为1的正方形拼成的矩形.
,宽为1的矩形,俯视图为两个边长为1的正方形拼成的矩形.
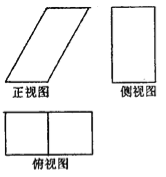
(1)求该几何体的体积![]() ;
;
(2)求该几何体的表面积![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A. 平行于同一个平面的两个平面平行
B. 平行于同一直线的两个平面平行
C. 垂直于同一个平面的两条直线平行
D. 垂直于同一条直线的两个平面平行
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com