
分析 由韦达定理得a3a15=8,由等比数列通项公式性质得:${{a}_{9}}^{2}={a}_{3}{a}_{15}={a}_{1}{a}_{17}$=8,由此能求出$\frac{{{a_1}{a_{17}}}}{a_9}$的值.
解答 解:∵在等比数列{an}中,a3,a15是方程x2-6x+8=0的根,
∴a3a15=8,
解方程x2-6x+8=0,得$\left\{\begin{array}{l}{{a}_{3}=2}\\{{a}_{15}=4}\end{array}\right.$或$\left\{\begin{array}{l}{{a}_{3}=4}\\{{a}_{15}=2}\end{array}\right.$,
∴a9>0,
由等比数列通项公式性质得:${{a}_{9}}^{2}={a}_{3}{a}_{15}={a}_{1}{a}_{17}$=8,
∴$\frac{{{a_1}{a_{17}}}}{a_9}$=a9=$\sqrt{8}=2\sqrt{2}$.
故答案为:2$\sqrt{2}$.
点评 本题考查等比数列中两项积与另一项的比值的求法,是基础题,解题时要认真审题,注意等比数列的性质的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
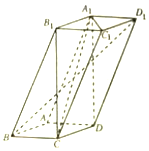 如图,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面为边长为1的正方形,侧棱AA1=2
如图,四棱柱ABCD-A1B1C1D1中,A1D⊥平面ABCD,底面为边长为1的正方形,侧棱AA1=2查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若点P∈α,P∈β且α∩β=l,则P∈l | |
| B. | 三点A,B,C能确定一个平面 | |
| C. | 若直线a∩b=A,则直线a与b能够确定一个平面 | |
| D. | 若点A∈l,B∈l,且A∈α,B∈α,则l?α |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | [1,+∞) | C. | (-1,1) | D. | [0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2=1,则x=1”的否定形式为:“若x2=1,则x≠1”. | |
| B. | 命题“若x2+y2=0,则x=y=0”的逆否命题为真. | |
| C. | △ABC中,sinA>sinB是A>B的充要条件. | |
| D. | 若向量$\overrightarrow{a}$,$\overrightarrow{b}$满足$\overrightarrow{a}$•$\overrightarrow{b}$>0,则$\vec a$与$\vec b$的夹角为锐角. |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com