
【题目】如图,在直三棱柱ABC—A1B1C1中,AB=BC=BB1, ![]() ,D为AC上的点,B1C∥平面A1BD;
,D为AC上的点,B1C∥平面A1BD;
(1)求证:BD⊥平面![]() ;
;
(2)若![]() 且
且![]() ,求三棱锥A-BCB1的体积.
,求三棱锥A-BCB1的体积.
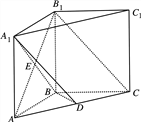
【答案】(1)见解析;(2)![]()
【解析】【试题分析】(1)运用线面垂直判定定理推证;(2)先求三棱锥的高与底面面积再运用三棱锥的体积公式求解:
(1)连结ED,
∵平面AB1C∩平面A1BD=ED,B1C∥平面A1BD,
∴B1C∥ED,
∵E为AB1中点,∴D为AC中点,
∵AB=BC, ∴BD⊥AC①
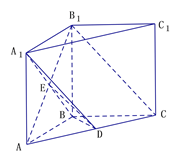
【法一】:由A1A⊥平面ABC, ![]() 平面ABC,得A1A⊥BD②,
平面ABC,得A1A⊥BD②,
由①②及A1A、AC是平面![]() 内的两条相交直线,得BD⊥平面
内的两条相交直线,得BD⊥平面![]() .
.
【法二】:由A1A⊥平面ABC,A1A![]() 平面
平面![]()
∴平面![]() ⊥平面ABC ,又平面
⊥平面ABC ,又平面![]()
![]() 平面ABC=AC,得BD⊥平面
平面ABC=AC,得BD⊥平面![]() .
.
(2)由![]() 得BC=BB1=1,
得BC=BB1=1,
由(1)知![]() ,又
,又![]() 得
得![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]()


科目:高中数学 来源: 题型:
【题目】在四棱柱![]() 中,
中, ![]() 底面
底面![]() ,底面
,底面![]() 为菱形,
为菱形, ![]() 为
为![]() 与
与![]() 交点,已知
交点,已知![]() ,
,![]() .
.

(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求证: ![]() ∥平面
∥平面![]() ;
;
(Ⅲ)设点![]() 在
在![]() 内(含边界),且
内(含边界),且![]()
![]() ,说明满足条件的点
,说明满足条件的点![]() 的轨迹,并求
的轨迹,并求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某地区儿童的身高与体重的一组数据,我们用两种模型①![]() ,②
,②![]() 拟合,得到回归方程分别为
拟合,得到回归方程分别为![]() ,
, ![]() ,作残差分析,如表:
,作残差分析,如表:
身高 | 60 | 70 | 80 | 90 | 100 | 110 |
体重 | 6 | 8 | 10 | 14 | 15 | 18 |
| 0.41 | 0.01 | 1.21 | -0.19 | 0.41 | |
| -0.36 | 0.07 | 0.12 | 1.69 | -0.34 | -1.12 |
(Ⅰ)求表中空格内的值;
(Ⅱ)根据残差比较模型①,②的拟合效果,决定选择哪个模型;
(Ⅲ)残差大于![]() 的样本点被认为是异常数据,应剔除,剔除后对(Ⅱ)所选择的模型重新建立回归方程.
的样本点被认为是异常数据,应剔除,剔除后对(Ⅱ)所选择的模型重新建立回归方程.
(结果保留到小数点后两位)
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计分别为
的斜率和截距的最小二乘法估计分别为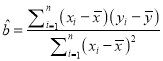 ,
, ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com