Question

13．已知函数f（x）=1nx-tx．
（1）若f（x）在（2，+∞）为增函数，求t的取值范围；
（2）讨论函数f（x）的零点的个教．

Answer 1

分析 （1）先求出函数f（x）的导数，问题转化为t＞$\frac{1}{x}$在x∈（2，+∞）上恒成立，解出即可；
（2）作函数g（x）=lnx与函数h（x）=tx的图象，从而求导，从而求解．

解答 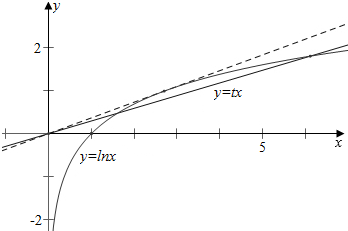解：（1）函数f（x）=lnx-tx的定义域为（0，+∞）．
∵f（x）在（2，+∞）上为增函数，
∴f′（x）=$\frac{1}{x}$-t＞0在x∈（2，+∞）上恒成立，
即t＜$\frac{1}{x}$在x∈（2，+∞）上恒成立，
∵0＜$\frac{1}{x}$＜$\frac{1}{2}$，∴t≤，
∴t的取值范围为（-∞，0]；
（2）令f（x）=1nx-tx=0，
得：lnx=tx，
令g（x）=lnx，h（x）=tx，
讨论函数f（x）的零点的个数问题转化为讨论g（x）和h（x）的交点问题，
直线h（x）与g（x）=lnx相切，设切点为（x，lnx），
g′（x）=$\frac{1}{x}$，则$\frac{1}{x}$=$\frac{lnx}{x}$，
故x=e；
故k_l=$\frac{1}{e}$，
故0＜t＜$\frac{1}{e}$时，图象有2个交点，即函数f（x）有2个零点，
t=$\frac{1}{e}$或t≤0时，图象有1个交点，即函数f（x）有1个零点，
t＞$\frac{1}{e}$时，图象没有交点，即函数f（x）没有零点．

点评 本题考查了学生的作图能力与应用图象的能力，同时考查了导数的几何意义的应用．