练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】执行右侧的程序框图,当输入的x的值为4时,输出的y的值2,则空白判断框中的条件可能为（ ）

    A. B. C. D.

    【答案】C

    【解析】方法一：当x=4,输出y=2,则由y=log2x输出，需要x>4，

    故选C.

    方法二：若空白判断框中的条件x>3，输入x=4，满足4>3，输出y=4+2=6，不满足，故A错误，

    若空白判断框中的条件x>4,输入x=4,满足4=4,不满足x>3,输出y=y=log24=2，故B正确；

    若空白判断框中的条件x4，输入x=4，满足4=4，满足x4，输出y=4+2=6，不满足，故C错误，

    若空白判断框中的条件x5，输入x=4，满足45，满足x5，输出y=4+2=6，不满足，故D错误，

    故选C.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在多面体中， 平面， 平面，且是边长为4的等边三角形， ， 与平面所成角的余弦值为， 是线段上一点．

    （Ⅰ）若是线段的中点，证明：平面平面；

    （Ⅱ）求二面角的平面角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，P是直线x=4上一动点，以P为圆心的圆Γ经定点B（1，0），直线l是圆Γ在点B处的切线，过A（﹣1，0）作圆Γ的两条切线分别与l交于E，F两点．

    （1）求证：|EA|+|EB|为定值；

    （2）设直线l交直线x=4于点Q，证明：|EB||FQ|=|BF|EQ|．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知某运动员每次投篮命中的概率低于，现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率：先由计算器产生0到9之间取整数值的随机数，指定1，2，3，4表示命中，5，6，7，8，9，0表示不命中；再以每三个随机数为一组，代表三次投篮的结果，经随机模拟产生了如下20组随机数：

    907 966 191 925 271 932 812 458 569 683

    431 257 393 027 556 488 730 113 537 989

    据此估计，该运动员三次投篮恰有两次命中的概率为（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】第32届夏季奥林匹克运动会将于2020年在日本东京举行，下表是五届奥运会中国代表团和俄罗斯代表团获得的金牌数的统计数据（单位：枚）．

    第30届伦敦

    第29届北京

    第28届雅典

    第27届悉尼

    第26届亚特兰大

    中国

    38

    51

    32

    28

    16

    俄罗斯

    24

    23

    27

    32

    26

    （Ⅰ）根据表格中两组数据完成五届奥运会两国代表团获得的金牌数的茎叶图，并通过茎叶图比较两国代表团获得的金牌数的平均值及分散程度（不要求计算出具体数值，给出结论即可）；

    （Ⅱ）甲、乙、丙三人竞猜2020年中国代表团和俄罗斯代表团中的哪一个获得的金牌数多（假设两国代表团获得的金牌数不会相等），规定甲、乙、丙必须在两个代表团中选一个，已知甲、乙猜中国代表团的概率都为，丙猜中中国代表团的概率为，三人各自猜哪个代表团的结果互不影响，现让甲、乙、丙各猜一次，设三人中猜中国代表团的人数为，求的分布列及数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一个盒子里装有三张卡片，分别标记有数字1，2，3，这三张卡片除标记的数字外完全相同．随机有放回地抽取3次，每次抽取1张，将抽取的卡片上的数字依次记为a，b，c.求：

    (1)“抽取的卡片上的数字满足a＋b＝c”的概率；

    (2)“抽取的卡片上的数字a，b，c不完全相同”的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设甲、乙、丙3个乒乓球协会的运动员人数分别为27，9，18.现采用分层抽样的方法从这3个协会中抽取6名运动员组队参加比赛．

    (1)求应从这3个协会中分别抽取的运动员的人数．

    (2)将抽取的6名运动员进行编号，编号分别为A1，A2，A3，A4，A5，A6.现从这6名运动员中随机抽取2人参加双打比赛．

    ①用所给编号列出所有可能的结果；

    ②设事件A为“编号为A5和A6的2名运动员中至少有1人被抽到”，求事件A发生的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列命题正确的是__________．（写出所有正确命题的序号）

    ①已知，“且”是“”的充要条件；

    ②已知平面向量，“且”是“”的必要不充分条件；

    ③已知，“”是“”的充分不必要条件；

    ④命题：“，使且”的否定为：“，都有且”

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某手机厂商推出一次智能手机，现对500名该手机使用者（200名女性，300名男性）进行调查，对手机进行打分，打分的频数分布表如下：

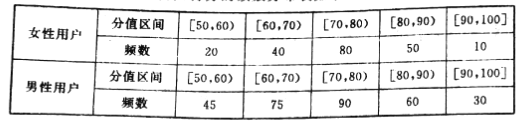
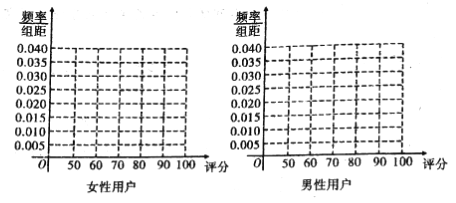
    （1）完成下列频率分布直方图，并比较女性用户和男性用户评分的方差大小（不计算具体值，给出结论即可）；

    （2）根据评分的不同，运用分层抽样从男性用户中抽取20名用户，在这20名用户中，从评分不低于80分的用户中任意取3名用户，求3名用户评分小于90分的人数的分布列和期望.

    查看答案和解析>>

    同步练习册答案