练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知定义在R上的函数f(x)的图象关于点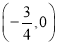成中心对称，对任意实数x都有f(x)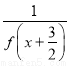＝－，且f(－1)＝1，f(0)＝－2，则f(0)＋f(1)＋…＋f(2013)＝________.

     

    －2

    【解析】由函数关于点对称可知，f(x)＋f＝0，所以f(1)＋f＝0，又f(x)＝－，所以＝＝－1，所以f(1)＝1，因为f(x)＝－，所以，所以f(1)＝1，因为f(x)＝－，所以f(x－3)＝－＝f(x)，即f(x)是以3为周期的函数，故f(3)＝f(0)＝－2，f(2)＝f(－1)＝1，所以f(0)＋f(1)＋f(2)＋…＋(2013)＝f(0)＋[f(1)＋f(2)＋f(3)]×671＝f(0)＝－2.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014年高考数学（理）二轮复习体系通关训练1-7练习卷（解析版） 题型：填空题

    已知x>0，y>0，lg 2x＋lg 8y＝lg 2，则的最小值为________．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮复习体系通关训练1-4练习卷（解析版） 题型：填空题

    设y＝f(x)是某港口水的深度y(米)关于时间t(时)的函数，其中0≤t≤24.下表是该港口某一天从0时至24时记录的时间t与水深y的关系：

    t

    0

    3

    6

    9

    12

    15

    18

    21

    24

    y

    5.0

    7.5

    5.0

    2.5

    5.0

    7.5

    5.0

    2.5

    5.0

    经长期观察，函数y＝f(t)的图象可以近似地看成函数y＝h＋Asin (ω＋φ)的图象，写出最能近似表示表中数据间对应关系的函数是______．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮复习体系通关训练1-3练习卷（解析版） 题型：填空题

    若 ＝3＋ln 2(a>1)，则a的值是______．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮复习体系通关训练1-3练习卷（解析版） 题型：选择题

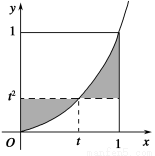
    如图，由曲线y＝x2和直线y＝t2(0<t<1)，x＝1，x＝0所围成的图形(阴影部分)的面积的最小值是(　　)．

     

    A. 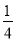B. 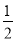C．1 D．2

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮复习体系通关训练1-2练习卷（解析版） 题型：选择题

    已知f(x)是定义在R上的奇函数，若对于x≥0，都有f(x＋2)＝f(x)，且当x∈[0,2]时，f(x)＝ex－1，则f(2 013)＋f(－2 014)＝(　　)．

    A．1－e B．e－1

    C．－1－e D．e＋1

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮复习体系通关训练1-2练习卷（解析版） 题型：选择题

    若奇函数f(x)在(0，＋∞)上的解析式是f(x)＝x(1－x)，则在(－∞，0)上，f(x)的解析式是(　　)．

    A．f(x)＝－x(1－x) B．f(x)＝x(1＋x)

    C．f(x)＝－x(1＋x) D．f(x)＝x(1－x)

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮复习体系通关训练1-11练习卷（解析版） 题型：填空题

    在区间[0,4]内随机取两个数a、b，则使得函数f(x)＝x2＋ax＋b2有零点的概率为________．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮复习体系通关 Word版训练3-x3练习卷（解析版） 题型：选择题

    已知向量a＝(2,1)，b＝(－2，k)，且a⊥(2a－b)，则实数k＝(　　)．

    A．－14 B．－6 C．6 D．14

     

    查看答案和解析>>

    同步练习册答案