
分析 根据函数和映射的定义分别进行判断即可.
解答 解:(1)设M=R,N=R,对应关系f:y=$\frac{1}{x}$,x∈M;当x=0时,没有对应元素,不是函数也不是映射.
(2)设M={平面上的点},N={(x,y)|x,y∈R},对应关系f:M中的元素对应它在平面上的坐标;
满足映射的定义,不是函数.
(3)设M={高年级的全体同学},N={0,1},对应关系f:M中的男生对应1,女生对应0;
满足映射的定义,不是函数.
(4)设M=R,N=R,对应关系:f(x)=2x2+1,x∈M;
满足映射的定义,也满足函数的定义.
(5)设M={1,4,9},N={-1,1,-2,2,3,-3},对应关系:M中的元素开平方.
M中的元素有两个对应关系,不满足对应的唯一性,不是映射也不是函数.
点评 本题主要考查函数和映射的判断,根据函数和映射的定义是解决本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
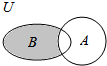 已知集合A={x|-$\sqrt{3}$≤x$\sqrt{3}$},B={x|-3≤x≤1},且A,B都是全集U的子集,则Venn图中阴影部分表示的集合为( )
已知集合A={x|-$\sqrt{3}$≤x$\sqrt{3}$},B={x|-3≤x≤1},且A,B都是全集U的子集,则Venn图中阴影部分表示的集合为( )| A. | {x|-$\sqrt{3}≤x≤1$} | B. | {x|-3≤x≤1} | C. | {x|-3$≤x≤-\sqrt{3}$} | D. | {x|1$≤x≤\sqrt{3}$} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com