
已知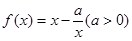 ,
,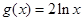 ,
,
(1)若对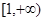 内的一切实数
内的一切实数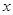 ,不等式
,不等式 恒成立,求实数
恒成立,求实数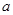 的取值范围;
的取值范围;
(2)当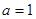 时,求最大的正整数
时,求最大的正整数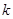 ,使得对
,使得对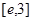 (
(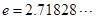 是自然对数的底数)内的任意
是自然对数的底数)内的任意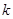 个实数
个实数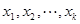 都有
都有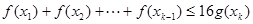 成立;
成立;
(3)求证:
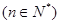 .
.
(1)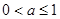 . (2)
. (2)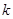 的最大值为
的最大值为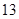 .
.
(3)证明(法一):先得到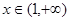 时,
时,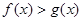 ,即
,即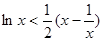 .
.
令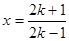 ,得
,得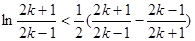 ,
,
化简得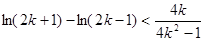 ,
, 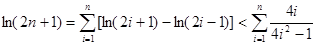 .
.
(法二)数学归纳法:
解析试题分析:(1)由 得
得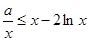 ,
,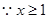 ,
,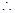 要使不等式
要使不等式 恒成立,必须
恒成立,必须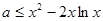 恒成立.
恒成立.
设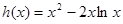 ,
, ,
,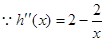 ,
,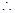 当
当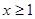 时,
时,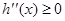 ,则
,则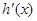 是增函数,
是增函数,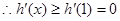 ,
,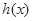 是增函数,
是增函数,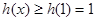 ,
,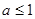 .
.
因此,实数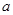 的取值范围是
的取值范围是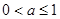 . 5分
. 5分
(2)当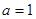 时,
时,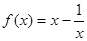 ,
,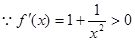 ,
,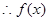 在
在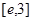 上是增函数,
上是增函数,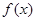 在
在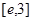 上的最大值为
上的最大值为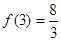 .
.
要对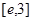 内的任意
内的任意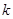 个实数
个实数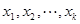 都有
都有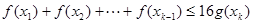
成立,必须使得不等式左边的最大值小于或等于右边的最小值, 当
当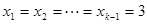 时不等式左边取得最大值,
时不等式左边取得最大值,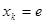 时不等式右边取得最小值.
时不等式右边取得最小值.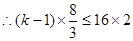 ,解得
,解得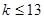 .
.
因此,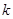 的最大值为
的最大值为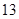 . 9分
. 9分
(3)证明(法一):当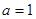 时,根据(1)的推导有,
时,根据(1)的推导有,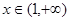 时,
时,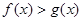 ,
,
即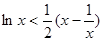 . 10分
. 10分
令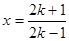 ,得
,得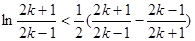 ,
,
化简得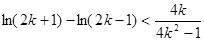 , 13分
, 13分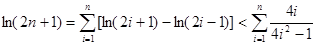 . 14分
. 14分
(法二)数学归纳法:当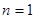 时,左边=
时,左边=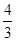 ,右边=
,右边=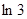 ,
,
根据(1)的推导有,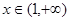 时,
时,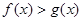 ,即
,即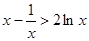 .
.
令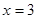 ,得
,得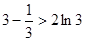 ,即
,即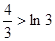 . 因此,
. 因此,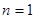 时不等式成立. 10分
时不等式成立. 10分
(另解: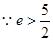 ,
,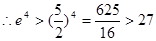 ,
,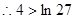 ,即
,即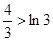 .)
.)
假设当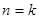 时不等式成立,即
时不等式成立,即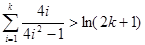 ,
,
则当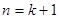 时,
时,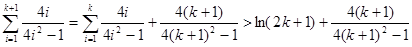 ,
,
要证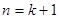 时命题成立,即证
时命题成立,即证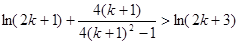


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com