
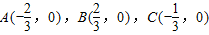 ,动P点满足
,动P点满足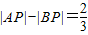 ,
,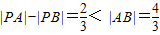 ,所以动点P的轨迹是A、B为焦点的双曲线的右支,由此能求出动点P的轨迹方程.
,所以动点P的轨迹是A、B为焦点的双曲线的右支,由此能求出动点P的轨迹方程. .此时y=±1,即弦长为2,满足题意.若m≠0,由
.此时y=±1,即弦长为2,满足题意.若m≠0,由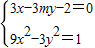 ,得
,得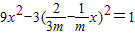 ,由此能推导出m=0.
,由此能推导出m=0. )=2(
)=2(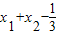 )=2,由此能求出m=0.
)=2,由此能求出m=0. 时,|BP|=1,|BC|=1,此时∠PCB=45°,∠PBC=90°,猜想λ=2.当x≠
时,|BP|=1,|BC|=1,此时∠PCB=45°,∠PBC=90°,猜想λ=2.当x≠ 时,设P(x,y),则
时,设P(x,y),则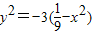 ,且tan∠PCB=
,且tan∠PCB= ,由此能够推导出存在λ=2,使得∠PBC=λ∠PCB.
,由此能够推导出存在λ=2,使得∠PBC=λ∠PCB. ,动P点满足
,动P点满足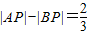 ,
, ,
, ,(x>a),
,(x>a), ,解得:
,解得: ,
,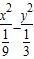 =1.(x>0).…(4分)
=1.(x>0).…(4分) .
. ,消去y,得
,消去y,得 ,
,

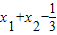 )=2(
)=2( )=2.
)=2.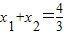
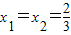 ,此时x1+x2=
,此时x1+x2= 满足.…(5分)
满足.…(5分)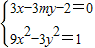 ,消去y得
,消去y得 ,
, .
. 时,|BP|=1,|BC|=1,
时,|BP|=1,|BC|=1, 时,设P(x,y),则
时,设P(x,y),则 ,
,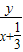 ,
, ,
,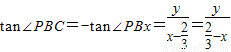 ,
,

科目:高中数学 来源: 题型:
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖南省郴州一中高二(上)期中数学试卷(理科)(解析版) 题型:解答题
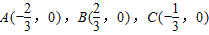 ,动P点满足
,动P点满足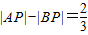 ,
,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com