
【题目】如图,某住宅小区的平面图呈圆心角![]() 为的扇形
为的扇形![]() ,小区的两个出入口设置在点
,小区的两个出入口设置在点![]() 及点
及点![]() 处,且小区里有一条平行于
处,且小区里有一条平行于![]() 的小路
的小路![]() 。
。

(1)已知某人从![]() 沿
沿![]() 走到
走到![]() 用了
用了![]() 分钟,从
分钟,从![]() 沿
沿![]() 走到
走到![]() 用了
用了![]() 分钟,若此人步行的速度为每分钟
分钟,若此人步行的速度为每分钟![]() 米,求该扇形的半径
米,求该扇形的半径![]() 的长(精确到
的长(精确到![]() 米)
米)
(2)若该扇形的半径为![]() ,已知某老人散步,从
,已知某老人散步,从![]() 沿
沿![]() 走到
走到![]() ,再从
,再从![]() 沿
沿![]() 走到
走到![]() ,试确定
,试确定![]() 的位置,使老人散步路线最长。
的位置,使老人散步路线最长。
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的离心率e=
的离心率e=![]() , 原点到过A(a,0),B(0,﹣b)两点的直线的距离是
, 原点到过A(a,0),B(0,﹣b)两点的直线的距离是![]() .
.
(1)求椭圆的方程;
(2)已知直线y=kx+1(k≠0)交椭圆于不同的两点E,F,且E,F都在以B为圆心的圆上,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的三个顶点
的三个顶点![]() ,其外接圆为圆
,其外接圆为圆![]() .
.
(1)若直线![]() 过点
过点![]() ,且被圆
,且被圆![]() 截得的弦长为
截得的弦长为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)对于线段![]() (包括端点)上的任意一点
(包括端点)上的任意一点![]() ,若在以
,若在以![]() 为圆心的圆上都存在不同的两点
为圆心的圆上都存在不同的两点![]() ,使得点
,使得点![]() 是线段
是线段![]() 的中点,求圆
的中点,求圆![]() 的半径
的半径![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查喜欢看书是否与性别有关,某校调查小组就“是否喜欢看书”这个问题,在全校随机调研了100名学生.
(1)完成下列![]() 列联表:
列联表:
喜欢看书 | 不喜欢看书 | 合计 | |
女生 | 15 | 50 | |
男生 | 25 | ||
合计 | 100 |
(2)能否在犯错率不超过0.025的前提下认为“喜欢看书与性别有关”.
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一某班的一次数学测试成绩的茎叶图和频率分布直方图因故都受到不同程度的损坏,但可见部分如下,据此解答如下问题: 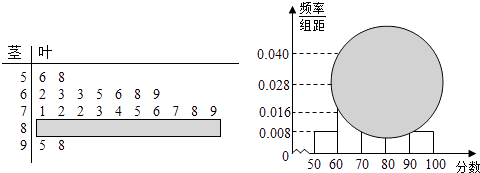
(Ⅰ)求分数在[50,60)的频率及全班人数;
(Ⅱ)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间的矩形的高;
(Ⅲ)若规定:75(包含75分)分以上为良好,90分(包含90分)以上为优秀,要从分数在良好以上的试卷中任取两份分析学生失分情况,设在抽取的试卷中,分数为优秀的试卷份数为X,求X的概率分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com