
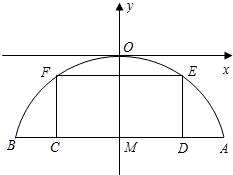
 有一座抛物线型拱桥,其水面宽AB为18米,拱顶O离水面AB的距离OM为8米,货船在水面上的部分的横断面是矩形CDEF,如图建立平面直角坐标系.
有一座抛物线型拱桥,其水面宽AB为18米,拱顶O离水面AB的距离OM为8米,货船在水面上的部分的横断面是矩形CDEF,如图建立平面直角坐标系.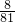 ,b=0,c=0.
,b=0,c=0.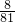 x2.(2分)
x2.(2分)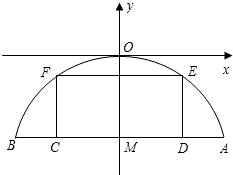
 ,则点E的纵坐标为
,则点E的纵坐标为 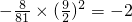
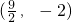 ,
,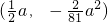 ,
,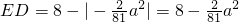
 a3(0<a<18).(7分)
a3(0<a<18).(7分)

科目:高中数学 来源: 题型:
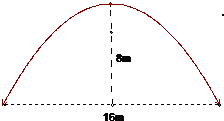 如图,河道上有一座抛物线型拱桥,在正常水位时,拱圈最高点距水面为8m,拱圈内水面宽16m.,为保证安全,要求通过的船顶部(设为平顶)与拱桥顶部在竖直方向上高度之差至少要有0.5m.
如图,河道上有一座抛物线型拱桥,在正常水位时,拱圈最高点距水面为8m,拱圈内水面宽16m.,为保证安全,要求通过的船顶部(设为平顶)与拱桥顶部在竖直方向上高度之差至少要有0.5m.| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
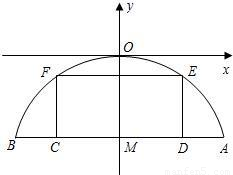
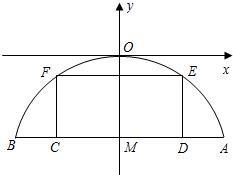 有一座抛物线型拱桥,其水面宽AB为18米,拱顶O离水面AB的距离OM为8米,货船在水面上的部分的横断面是矩形CDEF,如图建立平面直角坐标系.
有一座抛物线型拱桥,其水面宽AB为18米,拱顶O离水面AB的距离OM为8米,货船在水面上的部分的横断面是矩形CDEF,如图建立平面直角坐标系.查看答案和解析>>
科目:高中数学 来源:《第1章 集合与函数概念》2010年单元测试卷(5)(解析版) 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2012届温州十校联合体高二第一学期期末联考数学试卷(理科) 题型:解答题
本题10分)如图,河道上有一座抛物线型拱桥,在正常水位时,拱圈最高点距水面为8m,拱圈内水面宽16 m., 为保证安全,要求通过的船顶部(设为平顶)与拱桥顶部在竖直方向上高度之差至少要有0.5m.
(1)一条船船顶部宽4m,要使这艘船安全通过,则船在水面以上部分高不能超过多少米?
(2)近日因受台风影响水位暴涨2.7m,为此必须加重船载,降低船身,才能通过桥洞. 试问:一艘顶部宽 m,在水面以上部分高为4m的船船身应至少降低多少米才能安全通过?
m,在水面以上部分高为4m的船船身应至少降低多少米才能安全通过?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com