
【题目】设关于![]() 的方程
的方程![]() 有两个实根
有两个实根![]() ,函数
,函数![]() .
.
(1)求![]() 的值;
的值;
(2)判断![]() 在区间
在区间![]() 的单调性,并加以证明;
的单调性,并加以证明;
(3)若![]() 均为正实数,证明:
均为正实数,证明: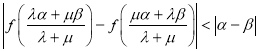
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为边长为2的菱形,
为边长为2的菱形,![]() ,
,![]() ,面
,面![]() 面
面![]() ,点
,点![]() 为棱
为棱![]() 的中点.
的中点.

(1)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 面
面![]() ,并说明理由;
,并说明理由;
(2)当二面角![]() 的余弦值为
的余弦值为![]() 时,求直线
时,求直线![]() 与平面
与平面![]() 所成的角.
所成的角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市规定,高中学生在校期间须参加不少于80小时的社区服务才合格.某校随机抽取20位学生参加社区服务的数据,按时间段![]() (单位:小时)进行统计,其频率分布直方图如图所示.
(单位:小时)进行统计,其频率分布直方图如图所示.
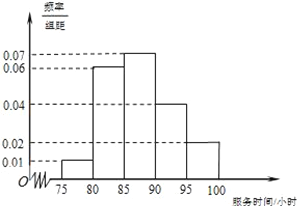
(1)求抽取的20人中,参加社区服务时间不少于90小时的学生人数;
(2)从参加社区服务时间不少于90小时的学生中任意选取2人,求所选学生的参加社区服务时间在同一时间段内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆周上依次排列着![]() 共2013个不同的点,每个点染红、蓝、绿三色之一.在以任意两个同色点为端点的圆弧上,与此两端点异色的点的个数为偶数的染色方法称为“好染色”问:所有好染色方法有多少种?
共2013个不同的点,每个点染红、蓝、绿三色之一.在以任意两个同色点为端点的圆弧上,与此两端点异色的点的个数为偶数的染色方法称为“好染色”问:所有好染色方法有多少种?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥O﹣ABCD中,OA⊥底面ABCD,且底面ABCD是边长为2的正方形,且OA=2,M,N分别为OA,BC的中点.
(1)求证:直线MN![]() 平面OCD;
平面OCD;
(2)求点B到平面DMN的距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com