
【题目】设关于x的一元二次方程![]() ,其中a,b是某范围内的随机数,分别在下列条件下,求上述方程有实根的概率.
,其中a,b是某范围内的随机数,分别在下列条件下,求上述方程有实根的概率.
(1)若随机数a,b∈{1,2,3,4,5,6};
(2)若a是从区间[0,5]中任取的一个数,b是从区间[2,4]中任取的一个数.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)设事件A为“方程x2+2ax+b2=0有实根”,当a≥0,b≥0时,方程x2+2ax+b2=0有实根的充要条件为a≥b,利用列举法能求出事件A发生的概率为P(A).
(2)试验的全部结果所构成的区域为{(a,b)|0≤a≤5,2≤b≤4}.构成事件A的区域为{(a,b)|0≤a≤5,2≤b≤4,a≥b},数形结合能求出所求的概率.
设事件A为方程![]() 有实根,
有实根,
当![]() ,
,![]() 时,方程
时,方程![]() 有实根的充要条件为
有实根的充要条件为![]() .
.
基本事件共有36个:(1,1),(1,2),(1,3),(1,4)(1,5),(1,6),(2,1),(2,2),(2,3),(2,4)(2,5),(2,6),(3,1)(3,2),(3,3),(3,4),(3,5),(3,6),(4,1)(4,2)(4,3)(4,4),(4,5),(4,6),(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),(6,1),(6,2),(6,3),(6,4)(6,5),(6,6),其中第一个数表示a的取值,第二个数表示b的取值.事件A中包含21个基本事件,
故事件A发生的概率为![]() 。
。
(2) 试验的全部结果所构成的区域为{(a,b)|0≤a≤5,2≤b≤4}.
构成事件A的区域为{(a,b)|0≤a≤5,2≤b≤4,a≥b},概率为两者的面积之比,
所以所求的概率为P(A)=![]() 。
。


科目:高中数学 来源: 题型:
【题目】如图:三棱锥P﹣ABC中,PA⊥底面ABC,若底面ABC是边长为2的正三角形,且PB与底面ABC所成的角为 ![]() .若M是BC的中点,求:
.若M是BC的中点,求: 
(1)三棱锥P﹣ABC的体积;
(2)异面直线PM与AC所成角的大小(结果用反三角函数值表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为直角梯形,且
为直角梯形,且![]() ,
,![]() ,平面
,平面![]() 底面
底面![]() ,
,![]() 为
为![]() 的中点,
的中点, ![]() 是棱
是棱![]() 的中点,
的中点, ![]() ,
,![]() .
.


(1)求证:![]() 平面BDM; (2)D到面PBC距离;
平面BDM; (2)D到面PBC距离;
(3)求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在钝角△ABC中,∠A为钝角,令 ![]() =
= ![]() ,
, ![]() =
= ![]() ,若
,若 ![]() =x
=x ![]() +y
+y ![]() (x,y∈R).现给出下面结论:
(x,y∈R).现给出下面结论:
①当x= ![]() 时,点D是△ABC的重心;
时,点D是△ABC的重心;
②记△ABD,△ACD的面积分别为S△ABD , S△ACD , 当x= ![]() 时,
时, ![]() ;
;
③若点D在△ABC内部(不含边界),则 ![]() 的取值范围是
的取值范围是 ![]() ;
;
④若 ![]() =λ
=λ ![]() ,其中点E在直线BC上,则当x=4,y=3时,λ=5.
,其中点E在直线BC上,则当x=4,y=3时,λ=5.
其中正确的有(写出所有正确结论的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)在定义域[﹣1,1]是奇函数,当x∈[﹣1,0]时,f(x)=﹣3x2 .
(1)当x∈[0,1],求f(x);
(2)对任意a∈[﹣1,1],x∈[﹣1,1],不等式f(x)≤2cos2θ﹣asinθ+1都成立,求θ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x﹣1|.
(1)若不等式f(x+ ![]() )≥2m+1(m>0)的解集为(﹣∞,﹣2]∪[2,+∞),求实数m的值;
)≥2m+1(m>0)的解集为(﹣∞,﹣2]∪[2,+∞),求实数m的值;
(2)若不等式f(x)≤2y+ ![]() +|2x+3|,对任意的实数x,y∈R恒成立,求实数a的最小值.
+|2x+3|,对任意的实数x,y∈R恒成立,求实数a的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
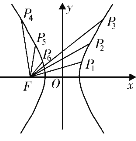
【题目】如图所示,F为双曲线C:![]() ﹣
﹣![]() =1的左焦点,双曲线C上的点Pi与P7﹣i(i=1,2,3)关于y轴对称,则|P1F|+|P2F|+|P3F|﹣|P4F|﹣|P5F|﹣|P6F|的值是( )
=1的左焦点,双曲线C上的点Pi与P7﹣i(i=1,2,3)关于y轴对称,则|P1F|+|P2F|+|P3F|﹣|P4F|﹣|P5F|﹣|P6F|的值是( )
A. 9 B. 16 C. 18 D. 27
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com