
已知数列{ }满足
}满足 =2,对于任意的n∈N都有
=2,对于任意的n∈N都有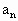 >0,且
(n+1)
>0,且
(n+1) .又知数列
.又知数列
(Ⅰ)求数列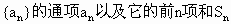 ;
;
(Ⅱ)求数列 ;
;
(Ⅲ)猜想 的大小关系,并说明理由.
的大小关系,并说明理由.
|
解:(Ⅰ)∵ ∴(n+1) ∴ ∴ ∴ ∴又 ∴
= (Ⅱ)∵ ∴
=
= (Ⅲ) 当n=1时, 当n=2时, 当n=3时, 当n=4时, 当n=5时, 当n=6时, 猜想,当n≥5时, 即 下面用数学归纳法证明:
≥
>
= ∴当n=k+1(k≥5)时, 由以上 当2≤n<5时, |


科目:高中数学 来源:2011届江苏省南京金陵中学高三预测卷2数学 题型:解答题
(本小题满分16分)
已知数列 满足
满足 =0,
=0,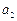 =2,
=2,
且对任意m,n∈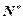 都有
都有 +
+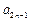 =
=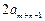 +
+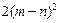
(1)求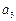 ,
,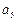 ;
;
(2)设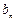 =
= -
-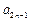 ( n∈
( n∈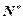 ),证明:
),证明: 是等差数列;
是等差数列;
(3)设 =(
=( -
-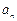 )
)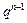 ( q≠0,n∈
( q≠0,n∈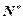 ),求数列的前n项的和
),求数列的前n项的和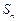 .
.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省高三预测卷2数学 题型:解答题
(本小题满分16分)
已知数列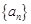 满足
满足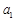 =0,
=0, =2,
=2,
且对任意m,n∈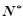 都有
都有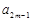 +
+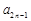 =
= +
+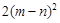
(1)求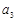 ,
, ;
;
(2)设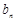 =
= -
-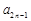 ( n∈
( n∈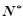 ),证明:
),证明: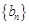 是等差数列;
是等差数列;
(3)设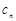 =(
=(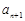 -
- )
)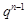 ( q≠0,n∈
( q≠0,n∈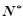 ),求数列的前n项的和
),求数列的前n项的和 .
.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省高三预测卷2数学 题型:解答题
(本小题满分16分)
已知数列 满足
满足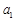 =0,
=0, =2,
=2,
且对任意m,n∈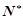 都有
都有 +
+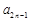 =
=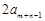 +
+
(1)求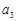 ,
,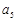 ;
;
(2)设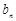 =
=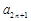 -
-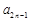 ( n∈
( n∈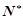 ),证明:
),证明: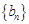 是等差数列;
是等差数列;
(3)设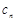 =(
=(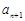 -
-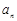 )
)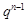 ( q≠0,n∈
( q≠0,n∈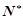 ),求数列的前n项的和
),求数列的前n项的和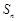 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com