
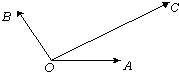
 如图,在平面内有三个向量
如图,在平面内有三个向量| OA |
| OB |
| OC |
| OA |
| OB |
| OA |
| OB |
| OC |
| OA |
| OC |
| 3 |
| OC |
| OA |
| OB |
| a |
|
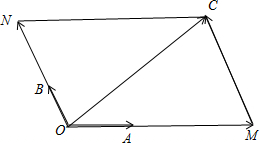 过点C分别作CM∥OB,CN∥OA,分别交射线OA、OB于M、N.
过点C分别作CM∥OB,CN∥OA,分别交射线OA、OB于M、N.| OC |
| OM |
| ON |
| OA |
| OB |
| OC |
| MC |
| OA |
| OB |
| OB |
| OC |
| 3 |
| 3 |
| OA |
| OB |
|
|
| a |
|


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,某海面上有O、A、B三个小岛(面积大小忽略不计),A岛在O岛的东北方向20
如图,某海面上有O、A、B三个小岛(面积大小忽略不计),A岛在O岛的东北方向20| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•湖南)在平面直角坐标系xOy中,将从点M出发沿纵、横方向到达点N的任一路径称为M到N的一条“L路径”.如图所示的路径MM1M2M3N与路径MN1N都是M到N的“L路径”.某地有三个新建居民区,分别位于平面xOy内三点A(3,20),B(-10,0),C(14,0)处.现计划在x轴上方区域(包含x轴)内的某一点P处修建一个文化中心.
(2013•湖南)在平面直角坐标系xOy中,将从点M出发沿纵、横方向到达点N的任一路径称为M到N的一条“L路径”.如图所示的路径MM1M2M3N与路径MN1N都是M到N的“L路径”.某地有三个新建居民区,分别位于平面xOy内三点A(3,20),B(-10,0),C(14,0)处.现计划在x轴上方区域(包含x轴)内的某一点P处修建一个文化中心.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com