
【题目】已知函数![]() 在定义域
在定义域![]() 上的导函数为
上的导函数为![]() ,若函数
,若函数![]() 没有零点,且
没有零点,且![]() ,当
,当![]() 在
在![]() 上与
上与![]() 在
在![]() 上的单调性相同时,则实数
上的单调性相同时,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】A
【解析】
由题意可知:f(x)为R上的单调函数,则f(x)﹣2019x为定值,由指数函数的性质可知f(x)为R上的增函数,则g(x)在[![]() ,
,![]() ]单调递增,求导,则g
]单调递增,求导,则g![]() (x)≥0恒成立,则k
(x)≥0恒成立,则k![]() sin(x
sin(x![]() )min,根据函数的正弦函数的性质即可求得k的取值范围.
)min,根据函数的正弦函数的性质即可求得k的取值范围.
解:若方程f![]() (x)=0无解,
(x)=0无解,
则 f′(x)>0或f′(x)<0恒成立,所以f(x)为R上的单调函数,
x∈R都有![]() ,
,
则![]() 为定值,
为定值,
设t=![]() ,则f(x)=t+
,则f(x)=t+![]() ,易知f(x)为R上的增函数,
,易知f(x)为R上的增函数,
∵g(x)=sinx﹣cosx﹣kx,
∴![]() ,
,
又g(x)与f(x)的单调性相同,
∴g(x)在R上单调递增,则当x∈[![]() ,
,![]() ],g
],g![]() (x)≥0恒成立,
(x)≥0恒成立,
当![]() 时,
时,![]() ,
,![]() ,
,
![]() ,
,
此时k≤﹣1,
故选:A.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
【题目】某校实行选科走班制度,张毅同学的选择是地理生物政治这三科,且生物在B层班级,该校周一上午选科走班的课程安排如下表所示,张毅选择三个科目的课各上一节,另外一节上自习,则他不同的选课方法有__________种
第一节 | 第二节 | 第三节 | 第四节 |
地理1班 | 化学A层3班 | 地理2班 | 化学A层4班 |
生物A层1班 | 化学B层2班 | 生物B层2班 | 历史B层1班 |
物理A层1班 | 生物A层3班 | 物理A层2班 | 生物A层4班 |
物理B层2班 | 生物B层1班 | 物理B层1班 | 物理A层4班 |
政治1班 | 物理A层3班 | 政治2班 | 政治3班 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在盒子里有大小相同,仅颜色不同的乒乓球共10个,其中红球4个,白球3个,蓝球3个。
(Ⅰ)现从中任取出一球确定颜色后放回盒子里,再取下一个球,重复以上操作,最多取3次,过程中如果取出蓝色球则不再取球,求:
①最多取两次就结束的概率;
②整个过程中恰好取到2个白球的概率;
(Ⅱ)若改为从中任取出一球确定颜色后不放回盒子里,再取下一个球。重复以上操作,最多取3次,过程中如果取出蓝色球则不再取球,则设取球的次数为随机变量![]() 求
求![]() 的分布列和数学期望,
的分布列和数学期望,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校20名同学的数学和英语成绩如下表所示:

将这20名同学的两颗成绩绘制成散点图如图:

根据该校以为的经验,数学成绩![]() 与英语成绩
与英语成绩![]() 线性相关.已知这
线性相关.已知这![]() 名学生的数学平均成绩为
名学生的数学平均成绩为![]() ,英语平均成绩
,英语平均成绩![]() ,考试结束后学校经过调查发现学号为
,考试结束后学校经过调查发现学号为![]() 的
的![]() 同学与学号为
同学与学号为![]() 的
的![]() 同学(分别对应散点图中的
同学(分别对应散点图中的![]() )在英语考试中作弊,故将两位同学的两科成绩取消.
)在英语考试中作弊,故将两位同学的两科成绩取消.
![]() 取消两位作弊同学的两科成绩后,求其余同学的数学成绩与英语成绩的平均数;
取消两位作弊同学的两科成绩后,求其余同学的数学成绩与英语成绩的平均数;
![]() 取消两位作弊同学的两科成绩后,求数学成绩x与英语成绩y的线性回归直线方程
取消两位作弊同学的两科成绩后,求数学成绩x与英语成绩y的线性回归直线方程![]() ,并据此估计本次英语考试学号为8的同学如果没有作弊的英语成绩.(结果保留整数)
,并据此估计本次英语考试学号为8的同学如果没有作弊的英语成绩.(结果保留整数)
附:![]() 位同学的两科成绩的参考数据:
位同学的两科成绩的参考数据:![]()
参考公式:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)的准线方程为x=﹣1.
(1)求抛物线C的方程;
(2)过抛物线C的焦点作直线l,交抛物线C于A,B两点,若线段AB中点的横坐标为6,求|AB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某校高三上学期期末数学考试成绩中,随机抽取了![]() 名学生的成绩得到如图所示的频率分布直方图:
名学生的成绩得到如图所示的频率分布直方图:
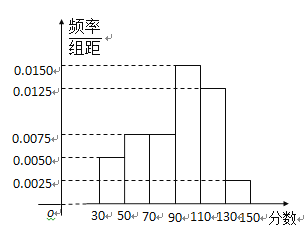
(1)根据频率分布直方图,估计该校高三学生本次数学考试的平均分;
(2)若用分层抽样的方法从分数在![]() 和
和![]() 的学生中共抽取
的学生中共抽取![]() 人,该
人,该![]() 人中成绩在
人中成绩在![]() 的有几人?
的有几人?
(3)在(2)中抽取的![]() 人中,随机抽取
人中,随机抽取![]() 人,求分数在
人,求分数在![]() 和
和![]() 各
各![]() 人的概率.
人的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com