
养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为12M,高4M。养路处拟建一个 更大的圆锥形仓库,以存放更多食盐。现有两种方案:一是新建的仓库的底面直径比原来大4M(高不变);二是
更大的圆锥形仓库,以存放更多食盐。现有两种方案:一是新建的仓库的底面直径比原来大4M(高不变);二是 高度增加4M(底面直径不变)。
高度增加4M(底面直径不变)。
(1)分别计算按这两种方案所建的仓库的体积;
(2)分别计算按这两种方案所建的仓库的表面积;
(3)哪个方案更经济些,说明理由.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
如图,在四棱锥P—ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=4,PA=3,点A在PD上的射影为点G,点E在AB上,平面PEC⊥平面PDC.
(1)求证:AG∥平面PEC;
(2)求AE的长;
(3)求二面角E—PC—A的正弦值.(本题满分14分)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
( 14分)如图,已知矩形ABCD中,AB=10,BC=6,将矩形沿对角线BD把△ABD折起,使A移到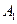 点,且
点,且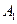 在平面BCD上的射影O恰好在CD上.
在平面BCD上的射影O恰好在CD上.
(Ⅰ)求证: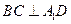 ;
;
(Ⅱ)求证:平面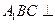 平面
平面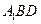 ;
;
(Ⅲ)求三棱锥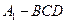 的体积.
的体积. 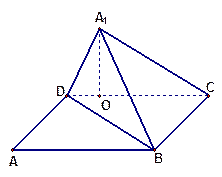
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(12分)如图所示,为了制作一个圆柱形灯笼,先要制作4个全等的矩形骨架,
总计耗用9.6米铁丝,再用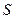 平方米塑料片制成圆柱的侧面和下底面(不安装上底面)。
平方米塑料片制成圆柱的侧面和下底面(不安装上底面)。
(Ⅰ)当圆柱底面半径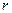 取何
取何 值时,
值时,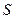 取得最大值?并求出该最大值(结果精确到0.01平方米);
取得最大值?并求出该最大值(结果精确到0.01平方米);
(Ⅱ)若要制作一个如图放置的,底面半径为0.3米的灯笼,请作出用于灯笼的三视图(作图时,不需考虑骨架等因素)。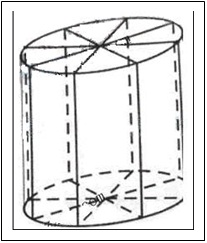
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图1,在平面内,ABCD 是
是 且
且 的菱形,
的菱形, 和
和 都是正方形。将两个正方形分别沿AD,CD折起,使
都是正方形。将两个正方形分别沿AD,CD折起,使 与
与 重合于点D1。设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧,设
重合于点D1。设直线l过点B且垂直于菱形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面ABCD同侧,设 (图2)。
(图2)。

(1)设二面角E – AC – D1的大小为q,若 ,求
,求 的取值范围;
的取值范围;
(2)在线段 上是否存在点
上是否存在点 ,使平面
,使平面 平面
平面 ,若存在,求出
,若存在,求出 分
分 所成的比
所成的比 ;若不存在,请说明理由。
;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分14分)
如图6所示,等腰三角形△ABC的底边AB=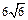 ,高CD=3.点E是线段BD上异于B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.
,高CD=3.点E是线段BD上异于B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.
记BE=x,V(x)表示四棱锥P-ACFE的体积。
(1)求V(x)的表达式;
(2)当x为何值时,V(x)取得最大值?
(3)当V(x)取得最大值时,求异面直线
AC与PF所成角的余弦值。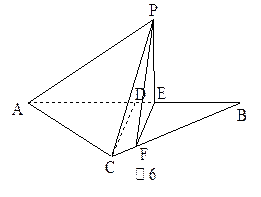
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com