
分析 运用正弦定理可得$max\left\{{\frac{sinA}{sinB},\frac{sinB}{sinC}}\right\}$=max{$\frac{a}{b}$,$\frac{b}{c}$},由A≤B≤C,可得a≤b≤c,即有$\frac{a}{b}$≤1,$\frac{b}{c}$≤1,再由a+b>c,两边同除以b,解不等式即可得到所求范围.
解答 解:由正弦定理可得,$\frac{a}{b}$=$\frac{sinA}{sinB}$,$\frac{b}{c}$=$\frac{sinB}{sinC}$,
即有$max\left\{{\frac{sinA}{sinB},\frac{sinB}{sinC}}\right\}$=max{$\frac{a}{b}$,$\frac{b}{c}$},
由A≤B≤C,可得a≤b≤c,
即有$\frac{a}{b}$≤1,$\frac{b}{c}$≤1,
当$\frac{a}{b}$≥$\frac{b}{c}$,即有max{$\frac{a}{b}$,$\frac{b}{c}$}=$\frac{a}{b}$,
由于a+b>c,可得$\frac{a+b}{b}$>$\frac{c}{b}$≥$\frac{b}{a}$,
即有($\frac{a}{b}$)2+$\frac{a}{b}$-1>0,
解得$\frac{\sqrt{5}-1}{2}$<$\frac{a}{b}$≤1;
当$\frac{a}{b}$<$\frac{b}{c}$,即有max{$\frac{a}{b}$,$\frac{b}{c}$}=$\frac{b}{c}$,
由于a+b>c,可得$\frac{a+b}{b}$>$\frac{c}{b}$,
即有$\frac{b}{c}$+1>$\frac{a+b}{b}$>$\frac{c}{b}$,
即为($\frac{b}{c}$)2+$\frac{b}{c}$-1>0,
解得$\frac{\sqrt{5}-1}{2}$<$\frac{b}{c}$≤1.
综上可得$max\left\{{\frac{sinA}{sinB},\frac{sinB}{sinC}}\right\}$的取值范围为($\frac{\sqrt{5}-1}{2}$,1].
点评 本题考查新定义的理解和运用,考查正弦定理的运用,以及三角形的两边之和大于第三边,考查运算能力,属于中档题.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图所示,在直三棱拄ABC-A1B1C1中,AA1=AB=AC=1,AB⊥AC,N是BC的中点,点P在直线A1B1上,且满足$\overrightarrow{{A}_{1}P}$=λ$\overrightarrow{{A}_{1}{B}_{1}}$,当直线PN与平面ABC所的角最大时,λ的值是( )
如图所示,在直三棱拄ABC-A1B1C1中,AA1=AB=AC=1,AB⊥AC,N是BC的中点,点P在直线A1B1上,且满足$\overrightarrow{{A}_{1}P}$=λ$\overrightarrow{{A}_{1}{B}_{1}}$,当直线PN与平面ABC所的角最大时,λ的值是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
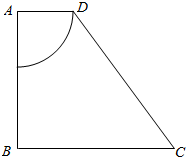 如图所示,在直角梯形ABCD 中,已知AB=4,BC=5,AD=2,以顶点A 为圆心,AD 为半径剪去一个扇形,剩下的部分绕AB 旋转一周形成一个几何体,指出该几何体的结构特征,并求该几何体的体积V 和表面积S.
如图所示,在直角梯形ABCD 中,已知AB=4,BC=5,AD=2,以顶点A 为圆心,AD 为半径剪去一个扇形,剩下的部分绕AB 旋转一周形成一个几何体,指出该几何体的结构特征,并求该几何体的体积V 和表面积S.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 直角三角形 | B. | 锐角三角形 | C. | 钝角三角形 | D. | 正三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}i$ | D. | $-\frac{1}{2}i$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com