Question

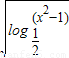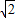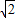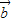①函数的零点所在的区间是（2，3）；②曲线y=4x-x³在点（-1，-3）处的切线方程是y=x-2；③将函数y=2^x+1的图象按向量a=（1，-1）平移后得到函数y=2^x+1的图象；④函数y=的定义域是（-，-1）∪（1，）⑤•＞0是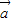、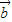的夹角为锐角的充要条件；以上命题正确的是    ．（注：把你认为正确的命题的序号都填上）

Answer 1

【答案】分析：①先求出f（2）f（3）＜0，再由二分法进行判断．
②根据导数的几何意义求出函数在x=-1处的导数，从而得到切线的斜率，再利用点斜式方程写出切线方程即可．
③先根据平移向量的坐标，利用函数图象的平移法则，我们可以求出平移后函数的解析式．
④根据偶次根号下的被开方数大于等于零，对数的真数大于零，列出不等式组，进行求解再用集合或区间的形式表示出来．
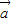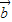⑤先看当 •＞0时，能否推出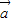、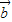的夹角是否为锐角，再看当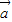、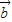的夹角为锐角时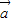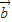，•＞0是否一定成立，然后根据充分条件、必要条件的定义进行判断．
解答：解：①由于f（2）f（3）=（-+lg2）（-+lg3）＜0，
根据二分法，得函数在区间（2，3]内存在零点．正确；
②y'=2-3x²
y'|_x=-1=-1
而切点的坐标为（-1，-3）
∴曲线y=4x-x³在x=1的处的切线方程为y=x-2；正确；
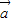③函数y=2^x+1的图象按=（1，-1）平移后得到的函数解析式为：y=2^x-1+3-1即y=2^x-1+2；故错；
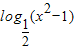④由≥0，且x²-1＞0，解得-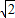≤x＜-1或1＜x≤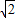，故错．
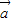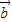⑤当 •＞0时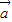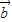，、的夹角可能为锐角，也可能为零角，故充分性不成立．
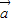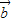当、的夹角为锐角时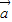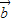，•＞0一定成立，故必要性成立．
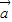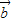综上，•＞0是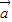、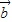的夹角为锐角的必要而不充分条件，故错．
故答案为：①②．
点评：本题考查命题的真假判断与应用，考查函数的零点问题、利用导数研究曲线上某点切线方程等，考查运算求解能力，属于基础题．