
 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案科目:高中数学 来源: 题型:解答题
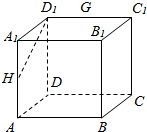 如图所示,在正方体ABCD-A1B1C1D1中,E、G、H分别是BC、C1D1、AA1、的中点.
如图所示,在正方体ABCD-A1B1C1D1中,E、G、H分别是BC、C1D1、AA1、的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 船上两根高5m的桅杆相距10m,一条30m长的绳子两端系在桅杆的顶上,并按如图所示的方式绷紧,假设绳子位于两根桅杆所在的平面内,求绳子与甲板接触点P到桅杆AB的距离.
船上两根高5m的桅杆相距10m,一条30m长的绳子两端系在桅杆的顶上,并按如图所示的方式绷紧,假设绳子位于两根桅杆所在的平面内,求绳子与甲板接触点P到桅杆AB的距离.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)=$\left\{\begin{array}{l}{2^x},x<0\\ 2{(x-1)^2}-1,x≥0\end{array}\right.$.
已知函数f(x)=$\left\{\begin{array}{l}{2^x},x<0\\ 2{(x-1)^2}-1,x≥0\end{array}\right.$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com