
【题目】设函数![]() .
.
(1)当![]() 时,对于一切
时,对于一切![]() ,函数
,函数![]() 在区间
在区间![]() 内总存在唯一零点,求
内总存在唯一零点,求![]() 的取值范围;
的取值范围;
(2)当![]() 时,数列
时,数列![]() 的前
的前![]() 项和
项和![]() ,若
,若![]() 是单调递增数列,求
是单调递增数列,求![]() 的取值范围;
的取值范围;
(3)当![]() ,
,![]() 时,函数
时,函数![]() 在区间
在区间![]() 内的零点为
内的零点为![]() ,判断数列
,判断数列![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 的增减性,并说明理由.
的增减性,并说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)递增,理由详见解析.
;(3)递增,理由详见解析.
【解析】
(1)分析出函数![]() 在区间
在区间![]() 上为增函数,由
上为增函数,由 可得出关于
可得出关于![]() 的不等式组,从而解出实数
的不等式组,从而解出实数![]() 的取值范围;
的取值范围;
(2)由题意得出![]() ,利用
,利用![]() 求出数列
求出数列![]() 的通项公式,然后由数列
的通项公式,然后由数列![]() 为递增数列,得出
为递增数列,得出![]() ,利用作差法得出关于
,利用作差法得出关于![]() 的不等式,从而得出实数
的不等式,从而得出实数![]() 的取值范围;
的取值范围;
(3)由题意得出![]() ,利用放缩法证明出
,利用放缩法证明出![]() ,然后利用函数
,然后利用函数![]() 在区间
在区间![]() 上单调递增得出
上单调递增得出![]() ,然后利用数列单调性的定义可得出数列
,然后利用数列单调性的定义可得出数列![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 的增减性.
的增减性.
(1)当![]() 时,
时,![]() 在
在![]() 上是增函数,
上是增函数,
由于函数![]() 在区间
在区间![]() 上有唯一零点,则
上有唯一零点,则 ,
,
![]() ,
,![]() ,
,![]() ,
,![]() .
.
因此,实数![]() 的取值范围是
的取值范围是![]() ;
;
(2)当![]() 时,
时,![]() ,则
,则![]() .
.
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
 .
.
由于数列![]() 是递增数列,对任意的
是递增数列,对任意的![]() ,
,![]() .
.
于是有![]() 且
且![]() 恒成立.
恒成立.
由![]() ,得
,得![]() ,解得
,解得![]() .
.
当![]() 时,由
时,由![]() ,得
,得![]() ,可得
,可得![]() .
.
构造数列![]() ,则
,则![]() ,
,
所以,数列![]() 为单调递减数列,当
为单调递减数列,当![]() 时,
时,![]() ,
,![]() .
.
综上所述,实数![]() 的取值范围是
的取值范围是![]() ;
;
(3)数列![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 为递增数列,证明如下:
为递增数列,证明如下:
当![]() ,
,![]() 时,
时,![]() ,该函数在
,该函数在![]() 上单调递增.
上单调递增.
由函数零点的定义可得 .
.
![]() ,
,![]() ,
,![]() ,
,
由于函数![]() 在
在![]() 上单调递增,所以,
上单调递增,所以,![]() .
.
因此,数列![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 为递增数列.
为递增数列.


科目:高中数学 来源: 题型:
【题目】已知![]() 为定义在实数集
为定义在实数集![]() 上的函数,把方程
上的函数,把方程![]() 称为函数
称为函数![]() 的特征方程,特征方程的两个实根
的特征方程,特征方程的两个实根![]() 、
、![]() (
(![]() ),称为
),称为![]() 的特征根.
的特征根.
(1)讨论函数![]() 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)已知![]() 为给定实数,求
为给定实数,求![]() 的表达式;
的表达式;
(3)把函数![]() ,
,![]() 的最大值记作
的最大值记作![]() ,最小值记作
,最小值记作![]() ,研究函数
,研究函数![]() ,
,![]() 的单调性,令
的单调性,令![]() ,若
,若![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为更好地落实农民工工资保证金制度,南方某市劳动保障部门调查了![]() 年下半年该市
年下半年该市![]() 名农民工(其中技术工、非技术工各
名农民工(其中技术工、非技术工各![]() 名)的月工资,得到这
名)的月工资,得到这![]() 名农民工月工资的中位数为
名农民工月工资的中位数为![]() 百元(假设这
百元(假设这![]() 名农民工的月工资均在
名农民工的月工资均在![]() (百元)内)且月工资收入在
(百元)内)且月工资收入在![]() (百元)内的人数为
(百元)内的人数为![]() ,并根据调查结果画出如图所示的频率分布直方图:
,并根据调查结果画出如图所示的频率分布直方图:
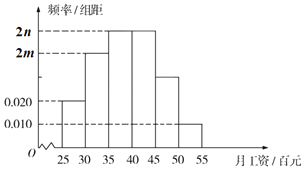
(Ⅰ)求![]() ,
,![]() 的值;
的值;
(Ⅱ)已知这![]() 名农民工中月工资高于平均数的技术工有
名农民工中月工资高于平均数的技术工有![]() 名,非技术工有
名,非技术工有![]() 名,则能否在犯错误的概率不超过
名,则能否在犯错误的概率不超过![]() 的前提下认为是不是技术工与月工资是否高于平均数有关系?
的前提下认为是不是技术工与月工资是否高于平均数有关系?
参考公式及数据: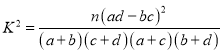 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.平行的两条直线的斜率一定存在且相等
B.平行的两条直线的倾斜角一定相等
C.垂直的两条直线的斜率之积为一1
D.只有斜率都存在且相等的两条直线才平行
查看答案和解析>>
科目:高中数学 来源: 题型:
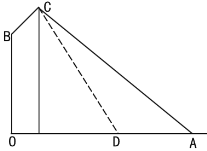
【题目】如图,在路边安装路灯:路宽![]() 米,灯杆长
米,灯杆长![]() 米,且与灯柱
米,且与灯柱![]() 成120°角,路灯采用锥形灯罩,灯罩轴线
成120°角,路灯采用锥形灯罩,灯罩轴线![]() 与灯杆垂直且正好通过道路路面的中线.
与灯杆垂直且正好通过道路路面的中线.
(1)求灯柱高![]() 的长度(精确到0.01米);
的长度(精确到0.01米);
(2)若该路灯投射出的光成一个圆锥体,该圆锥体母线与轴线的夹角是30°,写出路灯在路面上投射出的截面图形的边界是什么曲线?写出其相应的几何量(精确到0.01米).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A.在线性回归分析中,相关系数r的值越大,变量间的相关性越强
B.自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系
C.在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高
D.在问归分析中,![]() 为0.98的模型比
为0.98的模型比![]() 为0.80的模型拟合的效果好
为0.80的模型拟合的效果好
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某中学甲、乙两班各随机抽取![]() 名同学,测量他们的身高(单位:
名同学,测量他们的身高(单位:![]() ),所得数据用茎叶图表示如下,由此可估计甲、乙两班同学的身高情况,则下列结论正确的是( )
),所得数据用茎叶图表示如下,由此可估计甲、乙两班同学的身高情况,则下列结论正确的是( )

A. 甲班同学身高的方差较大 B. 甲班同学身高的平均值较大
C. 甲班同学身高的中位数较大 D. 甲班同学身高在![]() 以上的人数较多
以上的人数较多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正四棱锥![]() 的全面积为2,记正四棱锥的高为h.
的全面积为2,记正四棱锥的高为h.

(1)用h表示底面边长,并求正四棱锥体积V的最大值;
(2)当V取最大值时,求异面直线AB和PD所成角的大小.![]() 结果用反三角函数值表示
结果用反三角函数值表示![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com