设函数f(x)=x2-mlnx,h(x)=x2-x+a.
(1)当a=0时,f(x)≥h(x)在(1,+∞)上恒成立,求实数m的取值范围;
(2)当m=2时,若函数k(x)=f(x)-h(x)在[1,3]上恰有两个不同零点,求实数a的取值范围;
(3)是否存在实数m,使函数f(x)和函数h(x)在公共定义域上具有相同的单调性?若存在,求出m的值,若不存在,说明理由.
分析:(1)当a=0时,f(x)≥h(x)在(1,+∞)上恒成立,即:x
2-mlnx≥x
2-x,转化为即:m≤
在(1,+∞)上恒成立,从而得出实数m的取值范围.
(2)当m=2时,若函数k(x)=f(x)-h(x)在[1,3]上恰有两个不同零点,即:k(x)=x-2lnx-a,设y
1=x-2lnx,y
2=a,分别画出它们的图象,由图得实数a的取值范围.
(3)先假设存在实数m,使函数f(x)和函数h(x)在公共定义域上具有相同的单调性,由图可知,只须函数f(x)=x
2-mlnx在x=
处取得极小值即可.
解答: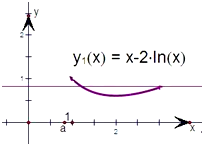
解:(1)当a=0时,f(x)≥h(x)在(1,+∞)上恒成立,
即:x
2-mlnx≥x
2-x,
mlnx≤x,即:m≤
在(1,+∞)上恒成立,
因为
在(1,+∞)上的最小值为:e,
∴m≤e.
实数m的取值范围:m≤e
(2)当m=2时,若函数k(x)=f(x)-h(x)在[1,3]上恰有两个不同零点,
即:k(x)=x-2lnx-a,
设y
1=x-2lnx,y
2=a,分别画出它们的图象,
由图得:
实数a的取值范围(2-2ln2,3-2ln3];
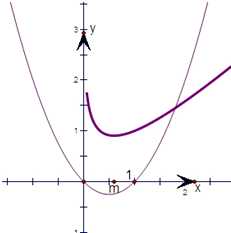
(3)假设存在实数m,使函数f(x)和函数h(x)在公共定义域上具有相同的单调性,
由图可知,只须函数f(x)=x
2-mlnx在x=
处取得极小值即可.
∵f(x)=x
2-mlnx
∴f′(x)=2x-m×
,将x=
代入得:
1-2m=0,
∴m=
故存在实数m=
,使函数f(x)和函数h(x)在公共定义域上具有相同的单调性.
点评:数形结合思想是解析函数图象交点个数、函数零点个数中最常用的方法,即画出满足条件的图象,然后根据图象直观的分析出答案,但数形结合的前提是熟练掌握各种基本初等函数的图象和性质.

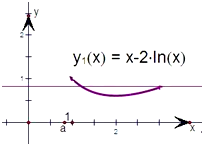 解:(1)当a=0时,f(x)≥h(x)在(1,+∞)上恒成立,
解:(1)当a=0时,f(x)≥h(x)在(1,+∞)上恒成立,

