
已知数列 ,
, 满足
满足 ,
, ,且对任意的正整数
,且对任意的正整数 ,
, 和
和 均成等比数列.
均成等比数列.
(1)求 、
、 的值;
的值;
(2)证明: 和
和 均成等比数列;
均成等比数列;
(3)是否存在唯一正整数 ,使得
,使得 恒成立?证明你的结论.
恒成立?证明你的结论.
(1)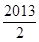 ,
,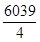 ;(2)详见解析;(3)详见解析.
;(2)详见解析;(3)详见解析.
解析试题分析:本题考查数列的求值,等比数列的证明和研究不等式的恒成立问题.(1)通过题设条件给出的数列关系,求出数列的初始值;(2)根据等比数列的定义,分别得到证明,其中应说明第一项不为零;(3)探求是否存在唯一的正整数 使得
使得 恒成立分两步求解,先通过数列
恒成立分两步求解,先通过数列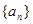 ,
, 的单调性得到
的单调性得到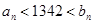 ,再证明证整数
,再证明证整数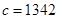 时唯一的,求解有关数列的综合问题,主要是要明确解题方向,合理利用数列的相关性质化难为易,化繁为简,同时还要注意解题步骤的规范性和严谨性.
时唯一的,求解有关数列的综合问题,主要是要明确解题方向,合理利用数列的相关性质化难为易,化繁为简,同时还要注意解题步骤的规范性和严谨性.
试题解析:(1)依题意,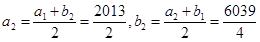 ;
;
(2)证明:依题意,对任意正整数 有
有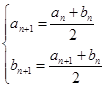 ,即
,即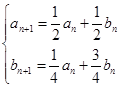 ,
,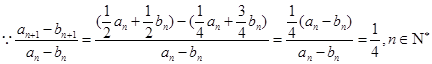 ,
,
又 ,
,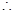 数列
数列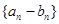 是首项为
是首项为 ,公比为
,公比为 的等比数列,
的等比数列, ,又
,又 ,
,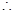 数列
数列 是首项为
是首项为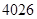 ,公比为
,公比为 的等比数列.
的等比数列.
(3)由(2)得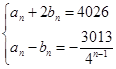 ,解得
,解得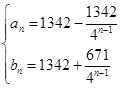 ,显然,数列
,显然,数列 是单调递增的数列,
是单调递增的数列, 是单调递减的数列,即存在正整数
是单调递减的数列,即存在正整数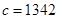 ,使得对任意的
,使得对任意的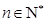 ,有
,有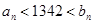 ,
,
又令 得
得 ,而
,而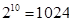 ,
, ,
,
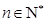 ,
,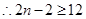 ,解得
,解得 ,即对任意的
,即对任意的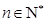 且
且 时,
时,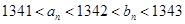 ,
,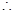 正整数
正整数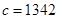 也是唯一的.
也是唯一的.
综上所述,存在唯一的正整数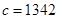 ,使得对任意的
,使得对任意的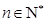 ,有
,有 .
.
考点:等差数列、等比数列的性质,数列不等式的恒成立问题.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:解答题
已知数列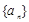 满足
满足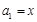 ,
, ,
, ,
,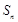 是数列
是数列 的前
的前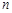 项和.
项和.
(1)若数列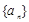 为等差数列.
为等差数列.
(ⅰ)求数列的通项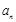 ;
;
(ⅱ)若数列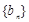 满足
满足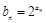 ,数列
,数列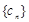 满足
满足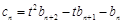 ,试比较数列
,试比较数列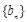 前
前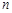 项和
项和 与
与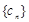 前
前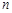 项和
项和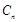 的大小;
的大小;
(2)若对任意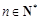 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
等比数列{an}的各项均为正数,且2a1+3a2=1,a32=9a2a6.
(1)求数列{an}的通项公式;
(2)设bn=log3a1+log3a2+…+log3an,求数列 的前n项和.
的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知数列 中,
中,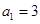 ,
, ,
,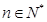 .
.
(1)证明:数列 是等比数列,并求数列
是等比数列,并求数列 的通项公式;
的通项公式;
(2)在数列 中,是否存在连续三项成等差数列?若存在,求出所有符合条件的项;若不存在,请说明理由;
中,是否存在连续三项成等差数列?若存在,求出所有符合条件的项;若不存在,请说明理由;
(3)若 且
且 ,
,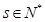 ,求证:使得
,求证:使得 ,
,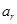 ,
, 成等差数列的点列
成等差数列的点列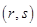 在某一直线上.
在某一直线上.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知无穷数列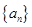 的前
的前 项和为
项和为 ,且满足
,且满足 ,其中
,其中 、
、 、
、 是常数.
是常数.
(1)若 ,
, ,
, ,求数列
,求数列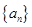 的通项公式;
的通项公式;
(2)若 ,
, ,
, ,且
,且 ,求数列
,求数列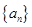 的前
的前 项和
项和 ;
;
(3)试探究 、
、 、
、 满足什么条件时,数列
满足什么条件时,数列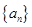 是公比不为
是公比不为 的等比数列.
的等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设集合W是满足下列两个条件的无穷数列 的集合:①对任意
的集合:①对任意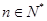 ,
,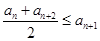 恒成立;②对任意
恒成立;②对任意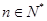 ,存在与n无关的常数M,使
,存在与n无关的常数M,使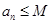 恒成立.
恒成立.
(1)若 是等差数列,
是等差数列,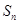 是其前n项和,且
是其前n项和,且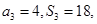 试探究数列
试探究数列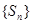 与集合W之间的关系;
与集合W之间的关系;
(2)设数列 的通项公式为
的通项公式为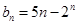 ,且
,且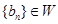 ,求M的取值范围.
,求M的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com