
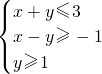 ,若0≤ax+by≤2,则
,若0≤ax+by≤2,则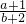 的取值范围为
的取值范围为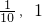 ]
]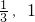 ]
]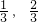 ]
]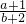 的取值范围.
的取值范围.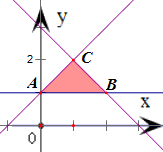 解:作出不等式组
解:作出不等式组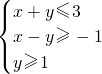 表示的平面区域,
表示的平面区域,
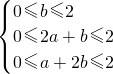 ,在aob坐标系
,在aob坐标系 中作出不等式组表示的平面区域,
中作出不等式组表示的平面区域, ,
, ),N(-
),N(- ,
, ),O是坐标原点
),O是坐标原点  表示点P(-1,-2)与Q(a,b)连线的斜率,
表示点P(-1,-2)与Q(a,b)连线的斜率, =1
=1 =10
=10 的取值范围为[1,10],
的取值范围为[1,10],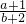 的取值范围为[
的取值范围为[ ,1].
,1].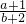 的取值范围.着重考查了二元一次不等式组表示的平面区域、直线的斜率和简单的线性规划等知识,属于基础题.
的取值范围.着重考查了二元一次不等式组表示的平面区域、直线的斜率和简单的线性规划等知识,属于基础题. 

 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:
| a2-b2 | a2+b2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com