
【题目】在平面直角坐标系xOy中,直线l经过点A(﹣1,0),其倾斜角是α,以原点O为极点,以x轴的非负半轴为极轴,与直角坐标系xOy取相同的长度单位,建立极坐标系.设曲线C的极坐标方程是ρ2=6ρcosθ﹣5.
(Ⅰ)若直线l和曲线C有公共点,求倾斜角α的取值范围;
(Ⅱ)设B(x,y)为曲线C任意一点,求 ![]() 的取值范围.
的取值范围.
【答案】解:(Ⅰ)曲线C的极坐标方程转化成直角坐标方程是C:x2+y2﹣6x+5=0,
由题意知直线l的斜率存在,设直线l:y=k(x+1),其中k=tanα.
联立 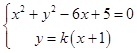
消去y得(1+k2)x2+2(k2﹣3)x+k2+5=0.
因为直线l和曲线C有交点,所以△=4(k2﹣3)2﹣4(1+k2)(k2+5)≥0,
即 ![]() ,
,
即 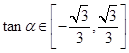 ,
,
所以 ![]() .
.
(Ⅱ)曲线C:x2+y2﹣6x+5=0即(x﹣3)2+y2=4的参数方程是 ![]() (θ为参数),
(θ为参数),
所以点B(x,y)的坐标可以写成(3+2cosθ,2sinθ),
所以 ![]() ,
,
因为sin(θ+ ![]() )∈[﹣1,1],
)∈[﹣1,1],
所以 ![]() x+y∈[3
x+y∈[3 ![]() ﹣4,3
﹣4,3 ![]() +4]
+4]
【解析】(Ⅰ)由x=ρcosθ,y=ρsinθ,代入曲线C的极坐标方程,可得曲线的直角坐标方程,联立直线l的方程,消去y,运用判别式大于等于0,可得斜率的范围,再由斜率公式,可得倾斜角的范围;(Ⅱ)求得曲线C的参数方程,运用两角和的正弦公式和正弦函数的值域,即可得到所求范围.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
【题目】为了调查患胃病是否与生活规律有关,在某地对![]() 名
名![]() 岁以上的人进行了调查,结果是:患胃病者生活不规律的共
岁以上的人进行了调查,结果是:患胃病者生活不规律的共![]() 人,患胃病者生活规律的共
人,患胃病者生活规律的共![]() 人,未患胃病者生活不规律的共
人,未患胃病者生活不规律的共![]() 人,未患胃病者生活规律的共
人,未患胃病者生活规律的共![]() 人.
人.
(1)根据以上数据列出![]() 列联表;
列联表;
(2)能否在犯错误的概率不超过![]() 的前提下认为“
的前提下认为“![]() 岁以上的人患胃病与否和生活规律有关系?”
岁以上的人患胃病与否和生活规律有关系?”
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形![]() 所在平面与以
所在平面与以![]() 为直径的圆所在平面垂直,
为直径的圆所在平面垂直,![]() 为
为![]() 中点,
中点,![]() 是圆周上一点,且
是圆周上一点,且![]() ,
,![]() ,
,![]() .
.

(1)求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(2)设点![]() 是线段
是线段![]() 上的点,且满足
上的点,且满足![]() ,若直线
,若直线![]() 平面
平面![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某研究型学习小组调查研究高中生使用智能手机对学习的影响,部分统计数据如下:
使用智能手机 | 不使用智能手机 | 合计 | |
学习成绩优秀 |
|
| |
学习成绩不优秀 |
|
| |
合计 |
(1)根据以上统计数据,你是否有![]() 的把握认为使用智能手机对学习有影响?
的把握认为使用智能手机对学习有影响?
(2)为进一步了解学生对智能手机的使用习惯,现从全校使用智能手机的高中生中(人数很多)随机抽取 ![]() 人,求抽取的学生中学习成绩优秀的与不优秀的都有的概率.
人,求抽取的学生中学习成绩优秀的与不优秀的都有的概率.
附:
|
|
|
|
|
|
|
|
|
|
|
|
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年,河北等8省公布了高考改革综合方案将采取“3+1+2”模式,即语文、数学、英语必考,然后考生先在物理、历史中选择1门,再在思想政治、地理、化学、生物中选择2门.为了更好进行生涯规划,甲同学对高一一年来的七次考试成绩进行统计分析,其中物理、历史成绩的茎叶图如图所示.

(1)若甲同学随机选择3门功课,求他选到物理、地理两门功课的概率;
(2)试根据茎叶图分析甲同学应在物理和历史中选择哪一门学科?并说明理由;
(3)甲同学发现,其物理考试成绩![]() (分)与班级平均分
(分)与班级平均分![]() (分)具有线性相关关系,统计数据如下表所示,试求当班级平均分为50分时,其物理考试成绩.
(分)具有线性相关关系,统计数据如下表所示,试求当班级平均分为50分时,其物理考试成绩.

参考数据: ![]() ,
,![]() ,
,![]() ,
,![]() .
.
参考公式:![]() ,
,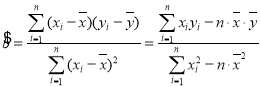 ,
,![]() (计算
(计算![]() 时精确到
时精确到![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某污水处理厂要在一个矩形污水处理池(ABCD)的池底水平铺设污水净化管道(管道构成Rt△FHE,H是直角项点)来处理污水.管道越长,污水净化效果越好.设计要求管道的接口H是AB的中点,E,F分别落在线段BC,AD上.已知AB=20米,AD=![]() 米,记∠BHE=
米,记∠BHE=![]() .
.

(1)试将污水净化管道的长度L表示为![]() 的函数,并写出定义域;
的函数,并写出定义域;
(2)当![]() 取何值时,污水净化效果最好?并求出此时管道的长度L.
取何值时,污水净化效果最好?并求出此时管道的长度L.
查看答案和解析>>
科目:高中数学 来源: 题型:
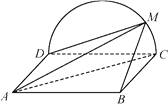
【题目】如图,边长为2的正方形![]() 所在的平面与半圆弧
所在的平面与半圆弧![]() 所在平面垂直,
所在平面垂直,![]() 是
是![]() 上异于
上异于![]() ,
,![]() 的点.
的点.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)当三棱锥![]() 体积最大时,求面
体积最大时,求面![]() 与面
与面![]() 所成二面角的正弦值.
所成二面角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com