
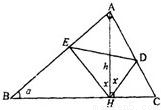
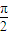 -α,∠DAH=α,∠HEA=π-x-(
-α,∠DAH=α,∠HEA=π-x-( -α)=
-α)=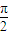 +α-x,同理∠ADH=π-α-x
+α-x,同理∠ADH=π-α-x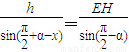 即EH=
即EH=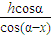
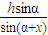
 ×DH×EHsin2x=
×DH×EHsin2x= ×
×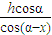 ×
×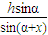 ×sin2x=
×sin2x= ×h2×
×h2×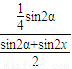 ×sin2x
×sin2x h2×(sin2α-
h2×(sin2α-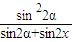 )
)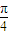 时,△DEH的面积最大为
时,△DEH的面积最大为 h2×(sin2α-
h2×(sin2α-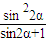 )
)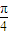 时,△DEH的面积最大为
时,△DEH的面积最大为 h2×(sin2α-
h2×(sin2α-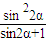 )
)

科目:高中数学 来源: 题型:
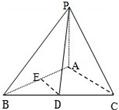 如图,在三棱锥P-ABC中,D、E分别是BC、AB的中点,PA⊥平面ABC,∠BAC=90°,AB≠AC,AC>AD,PC与DE所成的角为α,PD与平面ABC所成的角为β,二面角P-BC-A的平面角为γ,则α,β,γ的大小关系是( )
如图,在三棱锥P-ABC中,D、E分别是BC、AB的中点,PA⊥平面ABC,∠BAC=90°,AB≠AC,AC>AD,PC与DE所成的角为α,PD与平面ABC所成的角为β,二面角P-BC-A的平面角为γ,则α,β,γ的大小关系是( )| A、α<β<γ | B、α<γ<β | C、β<α<γ | D、γ<β<α |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
 (A)(不等式选讲)不等式log3(|x-4|+|x+5|)>a对于一切x∈R恒成立,则实数a的取值范围是
(A)(不等式选讲)不等式log3(|x-4|+|x+5|)>a对于一切x∈R恒成立,则实数a的取值范围是查看答案和解析>>
科目:高中数学 来源: 题型:
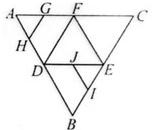
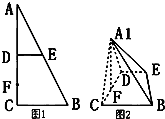 如图1,在Rt△ABC中,∠C=90°,D,E分别是AC,AB上的中点,
如图1,在Rt△ABC中,∠C=90°,D,E分别是AC,AB上的中点,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com