
已知函数f(x)=-x2+2ax+1-a在x∈[0,1]时有最大值2,求a的值.
a=2,或a=-1.
解析试题分析:解:原函数的对称轴为x=a,开口向下,①当a<0时,f(x)在[0,1]上单调递减,∴f(x)的最大值为f(0)=1-a=2,∴a=-1<0,∴a=-1符合题意,②当0≤a≤1时,f(x)的最大值为f(a)=-a2+2a2+1-a=a2-a+1=2,∴a= 或a=
或a=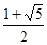 ∉[0,1],∴不合题意,无解,③当a>1时,f(x)在[0,1]上单调递增,∴f(x)的最大值为f(1)=-1+2a+1-a=a=2>1,∴a=2符合题意,综①②③得a=-1或a=2
∉[0,1],∴不合题意,无解,③当a>1时,f(x)在[0,1]上单调递增,∴f(x)的最大值为f(1)=-1+2a+1-a=a=2>1,∴a=2符合题意,综①②③得a=-1或a=2
考点:二次函数求最值问题
点评:本题考察二次函数求最值问题,注意对称轴与区间的位置关系,当对称轴于区间的位置关系不确定时,须分类讨论,从而得到原函数的单调性,进而可以求最值


 应用题作业本系列答案
应用题作业本系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com