
 对任意实数
对任意实数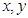 均有
均有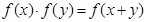 ,且当
,且当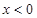 时
时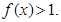
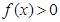 ;
; 为R上的减函数;
为R上的减函数;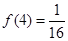 时, 对
时, 对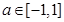 恒有
恒有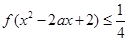 ,求实数
,求实数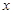 的取值范围.
的取值范围.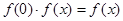 即
即 又
又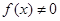
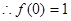
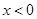 时,
时,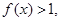
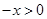
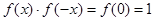 则
则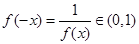
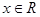 恒有
恒有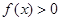
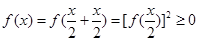
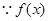 为非零函数
为非零函数 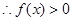
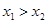 且
且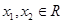
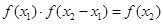 , 又
, 又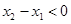 即
即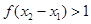
 又
又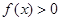
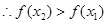
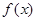 为R上的减函数
为R上的减函数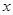 的取值范围为
的取值范围为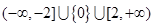
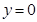 代入等式
代入等式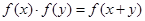 ,得出关于
,得出关于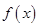 的方程,因为
的方程,因为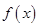 为非零函数,故
为非零函数,故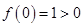 ,再令
,再令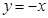 代入等式,可证
代入等式,可证 ,从而证明当
,从而证明当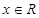 时,有
时,有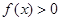 ;(2)着眼于减函数的定义,利用条件当
;(2)着眼于减函数的定义,利用条件当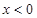 时,有
时,有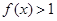 ,根据等式
,根据等式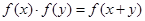 ,令
,令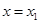 ,
,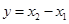 ,可得
,可得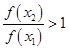 ,从而可证该函数为减函数.(3)根据
,从而可证该函数为减函数.(3)根据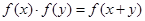 ,由条件
,由条件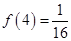 可求得
可求得 ,将
,将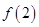 替换不等式中的
替换不等式中的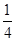 ,再根据函数的单调性可得
,再根据函数的单调性可得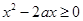 ,结合
,结合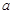 的范围,从而得解.
的范围,从而得解.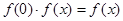 即
即 又
又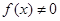
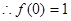
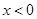 时,
时,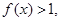
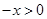
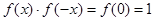 则
则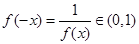
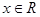 恒有
恒有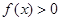 4分
4分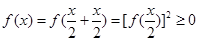
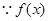 为非零函数
为非零函数 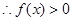
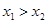 且
且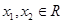
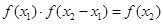 , 又
, 又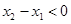 即
即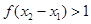
 又
又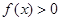
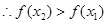
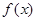 为R上的减函数 8分
为R上的减函数 8分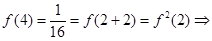 故
故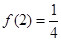 , 10分
, 10分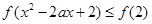
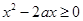 对
对 恒成立
恒成立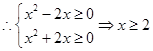 或
或 或
或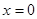
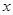 的取值范围为
的取值范围为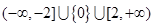 14分
14分

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com