
【题目】已知f(x)=x﹣2,g(x)=2x﹣5,则不等式|f(x)|+|g(x)|≤2的解集为;|f(2x)|+|g(x)|的最小值为 .
【答案】[ ![]() ,3];1
,3];1
【解析】解:∵f(x)=x﹣2,g(x)=2x﹣5, ∴|f(x)|+|g(x)|≤2,
即|x﹣2|+|2x﹣5|≤2,
x≥ ![]() 时,x﹣2+2x﹣5≤2,解得:
时,x﹣2+2x﹣5≤2,解得: ![]() ≤x≤3,
≤x≤3,
2<x< ![]() 时,x﹣2+5﹣2x≤2,解得:x≥1,
时,x﹣2+5﹣2x≤2,解得:x≥1,
x≤2时,2﹣x+5﹣2x≤2,解得:x≥ ![]() ,
,
综上,不等式的解集是[ ![]() ,3];
,3];
|f(2x)|+|g(x)|=|2x﹣4|+|2x﹣5|≥|2x﹣4﹣2x+5|=1,
故|f(2x)|+|g(x)|的最小值是1,
所以答案是:[ ![]() ,3],1.
,3],1.
【考点精析】关于本题考查的绝对值不等式的解法,需要了解含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号才能得出正确答案.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C1的参数方程为![]() (θ为参数),曲线C2的普通方程为
(θ为参数),曲线C2的普通方程为![]() ,以原点为极点,x轴的非负半轴为极轴建立极坐标系.
,以原点为极点,x轴的非负半轴为极轴建立极坐标系.
(1)求曲线C1的普通方程和C2的极坐标方程;
(2)若A,B是曲线C2上的两点,且OA⊥OB,求![]() +
+![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ax2﹣a﹣lnx,其中a∈R.
(1)讨论f(x)的单调性;
(2)当x∈(1,+∞)时,xf(x)+xe1﹣x>1恒成立,求a的取值范围.(其中,e=2.718…为自然对数的底数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l与抛物线![]() 交于点A,B两点,与x轴交于点M,直线OA,OB的斜率之积为
交于点A,B两点,与x轴交于点M,直线OA,OB的斜率之积为![]() .
.
(1)证明:直线AB过定点;
(2)以AB为直径的圆P交x轴于E,F两点,O为坐标原点,求|OE|![]() |OF|的值.
|OF|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥![]() 中,
中, ![]() 面
面![]() ,
, ![]() 是平行四边形,
是平行四边形, ![]() ,
, ![]() ,点
,点![]() 为棱
为棱![]() 的中点,点
的中点,点![]() 在棱
在棱![]() 上,且
上,且![]() ,平面
,平面![]() 与
与![]() 交于点
交于点![]() ,则异面直线
,则异面直线![]() 与
与![]() 所成角的正切值为__________.
所成角的正切值为__________.
【答案】![]()
【解析】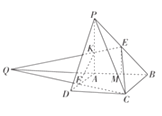
延长![]() 交
交![]() 的延长线与点Q,连接QE交PA于点K,设QA=x,
的延长线与点Q,连接QE交PA于点K,设QA=x,
由![]() ,得
,得![]() ,则
,则![]() ,所以
,所以![]() .
.
取![]() 的中点为M,连接EM,则
的中点为M,连接EM,则![]() ,
,
所以![]() ,则
,则![]() ,所以AK=
,所以AK=![]() .
.
由AD//BC,得异面直线![]() 与
与![]() 所成角即为
所成角即为![]() ,
,
则异面直线![]() 与
与![]() 所成角的正切值为
所成角的正切值为![]() .
.
【题型】填空题
【结束】
17
【题目】在极坐标系中,极点为![]() ,已知曲线
,已知曲线![]() :
: ![]() 与曲线
与曲线![]() :
: ![]() 交于不同的两点
交于不同的两点![]() ,
, ![]() .
.
(1)求![]() 的值;
的值;
(2)求过点![]() 且与直线
且与直线![]() 平行的直线
平行的直线![]() 的极坐标方程.
的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,点
,点![]() 满足
满足![]() ,记点
,记点![]() 的轨迹为
的轨迹为![]() .
.
(1)求轨迹![]() 的方程;
的方程;
(2)若直线![]() 过点
过点![]() 且与轨迹
且与轨迹![]() 交于
交于![]() 、
、![]() 两点.
两点.
(i)无论直线![]() 绕点
绕点![]() 怎样转动,在
怎样转动,在![]() 轴上总存在定点
轴上总存在定点![]() ,使
,使![]() 恒成立,求实数
恒成立,求实数![]() 的值.
的值.
(ii)在(i)的条件下,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列![]() 中,已知
中,已知![]() ,对于任意的
,对于任意的![]() ,有
,有![]() .
.
(1)求数列![]() 的通项公式.
的通项公式.
(2)若数列![]() 满足
满足![]() ,求数列
,求数列![]() 的通项公式.
的通项公式.
(3)设![]() ,是否存在实数
,是否存在实数![]() ,当
,当![]() 时,
时,![]() 恒成立?若存在,求实数
恒成立?若存在,求实数![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com