
【题目】在直角坐标系xOy中,直线l:y=t(t≠0)交y轴于点M,交抛物线C:y2=2px(p>0)于点P,M关于点P的对称点为N,连结ON并延长交C于点H.
(1)求![]() ;
;
(2)除H以外,直线MH与C是否有其它公共点?说明理由.
【答案】(1)2. (2)见解析.
【解析】试题分析:(1)根据题意,联立y=t 和抛物线方程可得P点坐标,进而得到N点坐标,再联立直线ON与抛物线方程可求得H点坐标,进而可求得![]() 的值;
的值;
(2)求出直线MH的方程,并代入抛物线方程中,求出只有一个公共点,从而得证。
试题解析:(1)由已知得M(0,t),P(![]() ,t).
,t).
又N为M关于点P的对称点,故N(![]() ,t),ON的方程为y=
,t),ON的方程为y=![]() x,
x,
代入y2=2px整理得px2-2t2x=0,解得x1=0,x2=![]() ,
,
因此H(![]() ,2t),∴N为OH的中点,即
,2t),∴N为OH的中点,即![]() =2.6分
=2.6分
(2)直线MH与C除H以外没有其它公共点.理由如下:
直线MH的方程为y-t=![]() x,即x=
x,即x=![]() (y-t).
(y-t).
代入y2=2px得y2-4ty+4t2=0,解得y1=y2=2t,即直线MH与C只有一个公共点.
∴除H以外直线MH与C没有其它公共点.


科目:高中数学 来源: 题型:
【题目】如图,在四棱柱![]() 中,
中, ![]() 平面
平面![]() ,底面
,底面![]() 为梯形,
为梯形, ![]() ,
, ![]() ,
, ![]() ,点
,点![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点.
的中点.

(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 与平面
与平面![]() 所成角的正弦值是
所成角的正弦值是![]() ,若存在,求
,若存在,求![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了净化空气,某科研单位根据实验得出,在一定范围内,每喷洒1个单位的净化剂,空气中释放的浓度y(单位:毫克/立方米)随着时间x(单位:天)变化的函数关系式近似为y=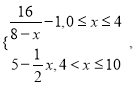 若多次喷洒,则某一时刻空气中的净化剂浓度为每次投放的净化剂在相应时刻所释放的浓度之和.由实验知,当空气中净化剂的浓度不低于4(毫克/立方米)时,它才能起到净化空气的作用.
若多次喷洒,则某一时刻空气中的净化剂浓度为每次投放的净化剂在相应时刻所释放的浓度之和.由实验知,当空气中净化剂的浓度不低于4(毫克/立方米)时,它才能起到净化空气的作用.
(1)若一次喷洒4个单位的净化剂,则净化时间可达几天?
(2)若第一次喷洒2个单位的净化剂,6天后再喷洒a(1≤a≤4)个单位的药剂,要使接下来的4天中能够持续有效净化,试求a的最小值(精确到0.1,参考数据: ![]() 取1.4).
取1.4).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知两个正方形ABCD和DCEF不在同一平面内,M,N分别为AB,DF的中点.
(1)若平面ABCD⊥平面DCEF,求直线MN与平面DCEF所成角的正弦值;
(2)用反证法证明:直线ME与BN是两条异面直线.

查看答案和解析>>
科目:高中数学 来源: 题型:
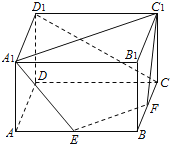
【题目】如图,在长方体ABCD﹣A1B1C1D1中,AA1=1,AB=AD=2,E、F分别是AB、BC的中点,证明A1、C1、F、E四点共面,并求直线CD1与平面A1C1FE所成的角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·北京高考)由四棱柱ABCDA1B1C1D1截去三棱锥C1B1CD1后得到的几何体如图所示.四边形ABCD为正方形,O为AC与BD的交点,E为AD的中点,A1E⊥平面ABCD.

(1)证明:A1O∥平面B1CD1;
(2)设M是OD的中点,证明:平面A1EM⊥平面B1CD1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com